Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ CH,DK vuông góc với AB
ΔCAB vuông tại C
=>CA^2+CB^2=AB^2
=>CA^2=26^2-10^2=576
=>CA=24(cm)
Xét ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*26=24*10=240
=>CH=120/13(cm)
ΔCAB vuông tại C có CH là đường cao
nên BH*BA=CB^2
=>BH=10^2/26=100/26=50/13(cm)
Xét ΔDKA vuông tại K và ΔCHB vuông tại H có
DA=CB
góc DAK=góc CBH
=>ΔDKA=ΔCHB
=>BH=KA=50/13(cm)
=>KH=26-50/13*2=238/13(cm)
Xét tứ giác DCHK có
DC//HK
DK//HC
=>DCHK là hình bình hành
=>DC=HK=238/13(cm)
S ABCD=1/2(DC+AB)*CH
=1/2(238/13+26)*120/13
=60/13*576/13
=34560/169cm2

-Gọi hình thang là ABCD, đáy nhỏ AB, đáy lớn CD, có AC⊥AD.
-Từ đỉnh A kẻ đường cao AH của hình thang. Khi đó, DH = \(\frac{50-14}{2}=18\) (cm) và CH = 50 - 18 = 32 (cm)
-Xét tam giác ACD vuông tại A, đường cao AH có:
\(AH^2=HD.HC=18.32=576\Rightarrow AH=24\)(cm)
-Xét tam giác AHD vuông tại H: \(AD=\sqrt{AH^2+DH^2}=\sqrt{24^2+18^2}=30\) (cm)
-Đã có hết các cạnh và đường cao của hình thang, áp dụng công thức tính ra chu vi và diện tích.

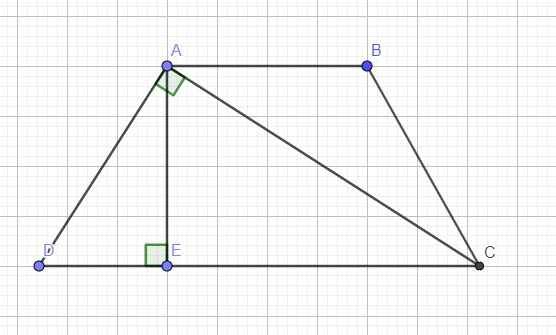
Kẻ đường cao góc AE \(\Rightarrow AE=AB\)
Lại có ABCD là hình thang cân \(\Rightarrow CD=AB+2DE=AE+2DE\Rightarrow DE=\dfrac{CD-AE}{2}=\dfrac{10-AE}{2}\)
\(EC=AB+DE=AE+DE=AE+\dfrac{10-AE}{2}=\dfrac{AE+10}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACD có:
\(AE^2=DE.EC\Leftrightarrow AE^2=\left(\dfrac{10-AE}{2}\right)\left(\dfrac{10+AE}{2}\right)\)
\(\Leftrightarrow4AE^2=100-AE^2\Rightarrow AE=2\sqrt{5}\) \(\Rightarrow AB=2\sqrt{5}\)
\(S_{ABCD}=\dfrac{1}{2}AE.\left(AB+CD\right)=\dfrac{1}{2}.2\sqrt{5}.\left(2\sqrt{5}+10\right)=...\)

Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),