Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2

\(\text{#3107}\)
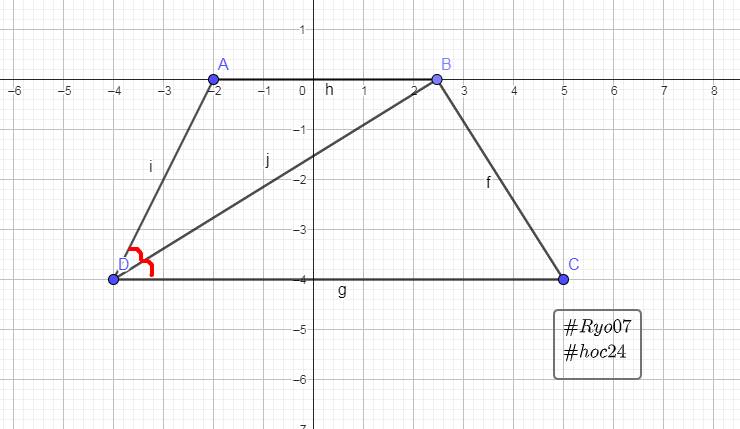
a)
Vì BD là tia phân giác của \(\widehat{\text{ADC}}\)
\(\Rightarrow\widehat{\text{ADB}}=\widehat{\text{CDB}}=\dfrac{1}{2}\widehat{\text{ADC}}\)
Mà ABCD là hình thang cân
\(\Rightarrow\widehat{\text{C}}=\widehat{\text{D}}\)
\(\Rightarrow\widehat{\text{C}}=2\widehat{\text{BDC}}\)
Xét `\Delta BDC:`
\(\widehat{\text{BDC}}+\widehat{\text{CBD}}+\widehat{\text{C}}=180^0\\ \Rightarrow\widehat{\text{BDC}}+90^0+2\widehat{\text{BDC}}=180^0\\ \Rightarrow3\widehat{\text{BDC}}=90^0\\ \Rightarrow\widehat{\text{BDC}}=30^0\)
Vì \(\widehat{\text{C}}=2\widehat{\text{BDC}}\)
\(\Rightarrow\widehat{\text{C}}=2\cdot30^0\\ \Rightarrow\widehat{\text{C}}=60^0\)
Vì $\widehat{C} = \widehat{D}$
\(\Rightarrow\widehat{\text{C}}=\widehat{\text{D}}=60^0\)
Vì ABCD là hình thang cân
\(\Rightarrow\widehat{\text{A}}+\widehat{\text{D}}=180^0\left(\text{2 góc trong cùng phía bù nhau}\right)\\ \Rightarrow\widehat{\text{A}}+60^0=180^0\\ \Rightarrow\widehat{\text{A}}=120^0\)
Vì \(\widehat{\text{A}}=\widehat{\text{B}}\left(\text{ABCD là hình thang cân}\right)\)
\(\Rightarrow\widehat{\text{A}}=\widehat{\text{B}}=120^0\)
Vậy, số đo các góc trong hình thang cân ABCD là: \(\widehat{\text{A}}=\widehat{\text{B}}=120^0;\widehat{\text{C}}=\widehat{\text{D}}=60^0.\)

Câu 1:
Gọi mỗi đinh của tứ giác là A, B, C, D. Các góc ngoài tương ứng lần lượt là A1, B1, C1, D1
Ta có: A+ B+ C+ D+ A1+ B1+ C1+ D1= 720 độ
Ma A+ B+ C+ D= 360 độ nên A1+ B1+ C1+ D1= 720 - 360= 360 độ
\(a,\) Vì \(AB=AD\) nên tam giác ABD cân tại A
Do đó \(\widehat{ADB}=\widehat{ABD}\)
Mà \(\widehat{ABD}=\widehat{BDC}\left(so.le.trong.vì.AB//CD\right)\)
\(\Rightarrow\widehat{ADB}=\widehat{BDC}\)
Vậy BD là p/g \(\widehat{ADC}\)
\(b,\) Vì ABCD là hình thang cân và BD là p/g nên \(\widehat{ADB}=\widehat{BDC}=\dfrac{1}{2}\widehat{ADC}=\dfrac{1}{2}\widehat{BCD}\)
Mà \(\widehat{BDC}+\widehat{BCD}=90^0\left(\Delta BDC\perp B\right)\)
\(\Rightarrow\dfrac{1}{2}\widehat{BCD}+\widehat{BCD}=90^0\Rightarrow\widehat{BCD}=60^0\)
\(\Rightarrow\widehat{BCD}=\widehat{ADC}=60^0\)
Ta có \(\widehat{BCD}+\widehat{ABC}=180^0\left(trong.cùng.phía.vì.AB//CD\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{BAD}=180^0-60^0=120^0\)