Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo nha
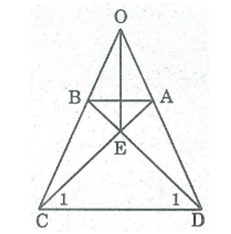
Xét tứ giác AEDO có góc A và D vuông=> AEDO nội tiếp đường tròn
=>góc AED+góc AOD=180(2 góc đối nhau) (1)
góc B chắn cung AD=> góc AOD=2*góc ABD mà tam giác ABI cân tại I nên góc ABD = góc BAC = 1/2 góc AOD=>góc ABD+BAC=AOD. Vì góc AID kề bù với góc AIB=> gócAID+góc AIB=180=AIB+ABD+BAC=AIB+AOD=>góc AID= góc AOD
từ (1)=> góc AED+góc AID=180(đpcm)

1.
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

-Sửa đề: F là giao của AC và BD.
EF cắt AB, CD lần lượt tại H,K.
\(\dfrac{AH}{BK}=\dfrac{AE}{BE}=\dfrac{AB}{DC}=\dfrac{BE}{CE}=\dfrac{BH}{CK}\)
\(\Rightarrow\dfrac{AH}{BK}=\dfrac{BH}{CK}=\dfrac{AB}{DC}\left(1\right)\)
\(\dfrac{AH}{CK}=\dfrac{AF}{CF}=\dfrac{AB}{CD}=\dfrac{BF}{DF}=\dfrac{BH}{DK}\)
\(\Rightarrow\dfrac{AH}{CK}=\dfrac{BH}{DK}=\dfrac{AB}{CD}\left(2\right)\)
-Từ (1) và (2) \(\Rightarrow\dfrac{AH}{CK}=\dfrac{AH}{BK}=\dfrac{BH}{CK}=\dfrac{BH}{DK}\)
\(\Rightarrow AH=BH;CK=DK\)
\(\Rightarrow\)H là trung điểm AB, K là trung điểm CD.

Ta có: ∠(ADC) = ∠(BCD) (gt)
⇒ ∠(ODC) = ∠(OCD)
⇒ΔOCD cân tại O (dhnb tam giác cân)
⇒ OC = OD
OB + BC = OA + AD
Mà AD = BC (hình thang ABCD cân)
⇒ OA = OB
Xét ΔADC và. ΔBCD:
AD = BC (hình thang ABCD cân )
AC = BD (hình thang ABCD cân)
CD chung
Do đó ΔADC và ΔBCD (c.c.c)
⇒ ∠D1= ∠C1
⇒ΔEDC cân tại E (dhnb tam giác cân)
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (hình thang ABCD cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
Mà OA = OB (cmt)
Nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.

Do ABCD là hình thang cân nên AD = BC, AC = BC, ˆD=ˆCD^=C^
Xét hai tam giác ADC và BCD, ta có: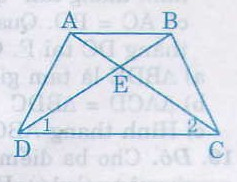
AD = BC (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra ˆC1=ˆD1C1^=D1^
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, ˆD=ˆCD^=C^ , DC là cạnh chung.
bn ơi trả lời sai đề
hok tốt