Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo link này ạ: 1. Cho hình vuông ABCD , E là điểm nằm trên CD. Gọi F là giao điểm của đường thẳng AE và BC. Qua E kẻ đường thẳng vuông... - Hoc24

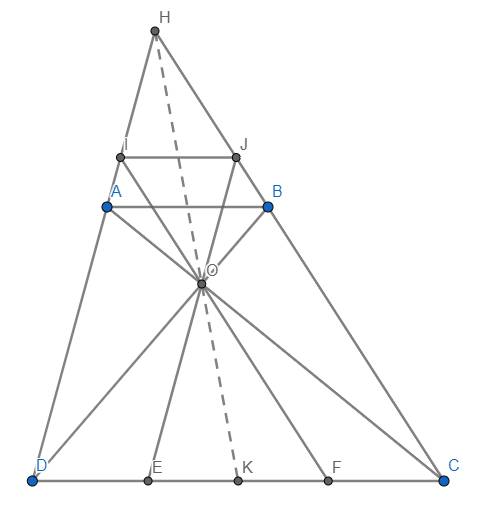
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)
Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)
c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)
Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\)
Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB
d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)
Ta có: \(\hept{\begin{cases}BE//AD\left(gt\right)\\AB//DE\left(gt\right)\end{cases}\Rightarrow ABED}\)là hình bình hành \(\Rightarrow\widehat{BEF}=\widehat{BAD}\left(t/c\right)\)
Tương tự, AFCB là hình bình hành \(\Rightarrow\widehat{AFE}=\widehat{ABC}\) (góc đối)
Mà \(\widehat{BAD}=\widehat{ABC}\)(tính chất hình thang cân)
\(\Rightarrow\widehat{BEF}=\widehat{AFE}\) Mà AB//FE nên ABEF là hình thang cân.
b, Bạn tự chứng minh được HA=HB,OA=OB,IA=IB
Do đó: H,O,I thẳng hàng (vì cùng nằm trên đường trung trực của đoạn AB) nên \(O\in IH\) (1)
\(\Delta IAB\)cân tại I có IH là đường trung tuyến nên IH đồng thời là đường cao
\(\Rightarrow IH\perp AB\Rightarrow IH\perp CD\) (AB//CD)
Mà \(IK\perp CD\left(gt\right)\Rightarrow I,H,K\)thẳng hàng \(\Rightarrow K\in IH\) (2)
Từ (1) và (2), ta được 4 điểm H,O,I,K thẳng hàng
Chúc bạn học tốt.