Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
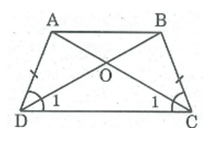
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

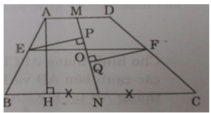
Ta có MA = MD, NC = NB (gt) và AD // BC.
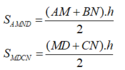
⇒ SAMND = SMCDN (các hình thang có các đáy bằng nhau và chung đường cao)
Do EF // AD nên đường cao từ E và F xuống AD bằng nhau, lại có AM = DM
⇒ SAEM = SDFM
Tương tự SBEN = SNFC
⇒ SAMNB - (SAEM + SBEN) = SDMNC - (SBEN + SNFC)
hay SEMN = SFMN
Hai tam giác trên có chung cạnh MN nên đường cao tương ứng bằng nhau hay EP = FQ
Xét ΔEPO và ΔFQO có:
∠EOP = ∠QOF (đối đỉnh)
EP = PQ (cmt)
∠EPO = ∠FQO = 90o
Do đó ΔEPO = ΔFQO (ch–gn) ⇒ OE = OF hay O là trung điểm của EF.

a: Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
=>ΔABC=ΔBAD
=>góc OBA=góc OAB
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
b: Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
EA+AD=ED
EB+BC=EC
mà EA=EB và AD=BC
nên ED=EC
EA=EB
OA=OB
=>EO là trung trực của AB
EC=ED
OC=OD
=>EO là trung trực của CD

a ) Xét ADC và BCD, ta có:
AD = BC (tính chất hình thang cân)
(ADC) = (BCD) (gt)
DC chung
Do đó: ADC = BCD (c.g.c) ⇒ =
Trong OCD ta có: = ⇒ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
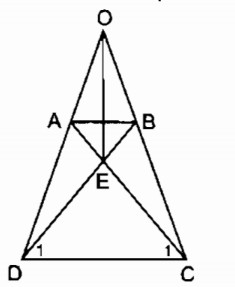
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.