Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD vuông tại A và ΔADC vuông tại D có
BA/AD=AD/DC
=>ΔBAD đồng dạng với ΔADC
b: ΔBAD đồng dạng với ΔADC
=>góc BDA=góc ACD
Xét ΔOAD và ΔDAC có
góc ODA=góc DCA
góc A chung
=>ΔOAD đồng dạng với ΔDAC
=>góc AOD=góc ADC=90 độ
=>AC vuông góc BD tại O
c: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>S OAB/S OCD=(AB/CD)^2=(4/9)^2=16/81

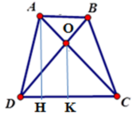
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.48 4 + 8 = 8 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 . 16 3 .8 = 64 3 c m 2
Đáp án: A

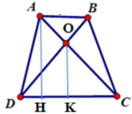
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.36 4 + 8 = 6 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 .4.8 = 16cm2
Đáp án: C

a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{ODC}=\widehat{OCD}\)
Xét ΔOCD có \(\widehat{ODC}=\widehat{OCD}\)
nên ΔCOD cân tại O
Qua O kẻ \(OH\perp AB\left(H\in AB\right)\) \(;OK\perp CD\left(K\in CD\right)\)
Do \(AB//CD\) nên \(O,H,K\) thẳng hàng.
Ta có:
\(AB//CD\rightarrow\frac{AB}{CD}=\frac{OA}{OC}=\frac{OB}{OD}\)
\(AH//KC\rightarrow\frac{OA}{OC}=\frac{OH}{OK}\)
\(\rightarrow\frac{OH}{OK}=\frac{AB}{CD}\)
\(\frac{S_{OAB}}{S_{OCD}}=\frac{\frac{1}{2}OH.AB}{\frac{1}{2}OK.CD}=\frac{OH.AB}{OK.CD}=\left(\frac{OH}{OK}\right)^2\)
\(\rightarrow\left(\frac{OH}{OK}\right)^2=\frac{64}{125}=\frac{OH}{OK}=\frac{8\sqrt{5}}{25}\)
\(\frac{S_{AOD}}{S_{DOC}}=\frac{AO}{OC}=\frac{OH}{OK}=\frac{8\sqrt{5}}{25}\rightarrow S_{AOD}=50\sqrt{5}\left(cm^2\right)\)