Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hình thang cân ABCD ( AB // CD )
\(\Rightarrow\hept{\begin{cases}\widehat{D}=\widehat{C}\\AD=BC\end{cases}\left(t/c\right)}\)
Xét \(\Delta ADH=\Delta BCK\)
\(\hept{\begin{cases}\widehat{AHD}=\widehat{BKC}\left(=90^o\right)\\AD=BC\left(cmt\right)\\\widehat{D}=\widehat{C}\left(cmt\right)\end{cases}}\)
\(\Rightarrow\Delta ADH=\Delta BCK\) ( ch - gn )
\(\Rightarrow AH=BK\) ( 2 cạnh tương ứng )
b) Vì \(\Delta ADH=\Delta BCK\left(cmt\right)\)
\(\Rightarrow DK=CK\) ( 2 cạnh tương ứng )
Chúc bạn học tốt !!!


Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:
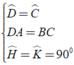
⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)

\(a,\widehat{D}=\widehat{C}=70^0\left(t/c.hthang.cân\right)\\ AB//CD\Rightarrow\widehat{A}+\widehat{D}=180^0\left(2.góc.trong.cùng.phía\right)\Rightarrow\widehat{A}=110^0\\ \widehat{A}=\widehat{B}=110^0\left(t/c.hthang.cân\right)\\ b,\left\{{}\begin{matrix}AD=BC\left(t/c.hthang.cân\right)\\\widehat{AHD}=\widehat{BKC}\left(=90^0\right)\\\widehat{D}=\widehat{C}\left(cm.trên\right)\end{matrix}\right.\Rightarrow\Delta AHD=\Delta BKC\left(ch-gn\right)\Rightarrow DH=CK\)

Lời giải:
Xét tam giác $ADH$ và $BCK$ có:
$\widehat{AHD}=\widehat{BKC}=90^0$
$\widehat{ADH}=\widehat{BCK}$ (do $ABCD$ là htc)
$AD=BC$ (do $ABCD$ là htc)
$\Rightarrow \triangle ADH=\triangle BCK$ (ch-gn)
$\Rightarrow DH=CK$
Áp dụng định lý Pitago cho tam giác $ADH$ vuông:
$AH=\sqrt{AD^2-DH^2}=\sqrt{10^2-6^2}=8$ (cm)
Từ tam giác bằng nhau ở trên suy ra $BK=AH=8$ (cm)

a: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔAHD=ΔBKC
Suy ra: DH=CK
b: Ta có: DH=CK
nên DH+HK=CK+HK
hay DK=HC


Tham khảo đường link này nha bạn:
https://i.imgur.com/aIUXkCl.jpg
Ta có hình vẽ:
Xét hai tam giác vuông ADH và BCK có:
AD = BC (ABCD là hình thang cân)
góc D = góc C (ABCD là hình thang cân)
=> tam giác ADH = tam giác BCK.
=> AH = BK.
*Ta có: AH vuông góc vs CD
Ta có: BK vuông góc vs CD
=> AH // BK
Xét tam giác ABK và tam giác AHK có:
AH = BK (Cmt)
AK: cạnh chung
góc HAK = góc AKB (AH // BK)
=> tam giác ABK = tam giác AHK.
=> HK = AB (hai cạnh tương ứng)
*Ta có:tam giác ADH = tam giác BCK (Cmt)
=> DH = CK.
Ta có: CD = DH + HK + KC
=> DH + CK = CD - HK
Mà HK = AB
=> DH + CK = CD - AB
Vì DH = CK
Nên DH + DH = CD - AB
=> DH = (CD - AB) / 2
hay CK + CK = CD - AB
=> CK = (CD - AB) / 2
===> DH = CK = (CD - AB) / 2.