Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho hình thang abcd (ab//cd) có góc b-c = 40 độ, và góc c-d bằng 20 độ tính các góc trong hình thang

Ta có :
\(\widehat{B}+\widehat{C}=180^o\)
(Hai góc trong cùng phía bù nhau ) [ vì AB // CD ]
Mà \(\widehat{B}-\widehat{C}=40^o\left(gt\right)\)
\(\Rightarrow\widehat{B}=40^o+\widehat{C}\)
\(\Rightarrow\widehat{B}+\widehat{C}=\widehat{C}+40^o+\widehat{C}\)
\(=\widehat{B}+\widehat{C}=2\widehat{C}+40^o=180^o\)
\(\Rightarrow\widehat{C}=180^o-40^o:2=70^o\)
Thay C vào \(\widehat{B}=40^o+\widehat{C}\)
Ta được : \(\widehat{B}=40^o+70^o\)
\(\Rightarrow\widehat{B}=110^o\)
Ta lại có :
\(\widehat{C}-\widehat{D}=20^o\)
Thay giá trị của C tìm được trên thay vào được :
\(70^o-\widehat{D}=20^o\)
\(\Rightarrow\widehat{D}=70-20=50^o\)
Vì ABCD là hình thang ( cũng là tứ giác lồi )
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Thay vào ta được :
\(\widehat{A}+110^o+70^o+50^o=360^o\)
\(\Rightarrow\widehat{A}=120^o\)
Vậy \(\widehat{A}=120^O\)
\(\widehat{B}=110^o\)
\(\widehat{C}=70^o\)
\(\widehat{D}=50^o\)

do AB song song với CD nên ta có \(A+D=180^0\text{ mà }A=D+40^0\Rightarrow D+40^0+D=180^0\Rightarrow\hept{\begin{cases}D=70^0\\A=110^0\end{cases}}\)
\(\Rightarrow C=\frac{A}{2}=55^0\Rightarrow B=180^0-55^0=125^0\)


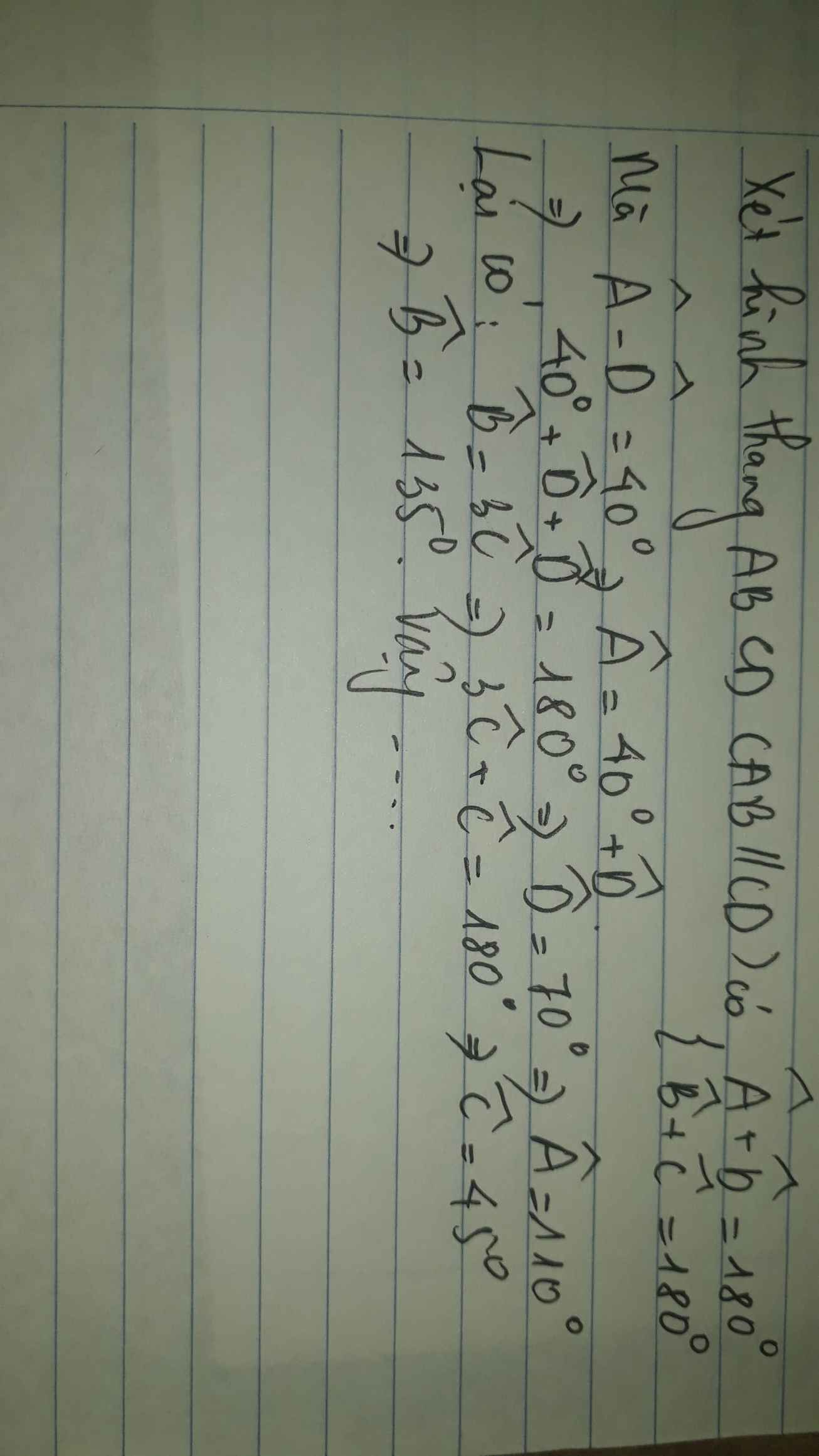
Ta có: góc B + góc C = 180 độ (AB//CD ; trong cùng phía)
=> góc B + góc C + góc B - góc C = 180 độ + 40 độ
=> 2 . góc B = 220 độ
=> góc B = 110 độ
=> góc C = 110 độ - 40 độ = 70 độ
Có: góc C - góc D = 20 độ
=> góc D = góc C - 20 độ = 70 độ - 20 độ = 50 độ
Mà góc A + góc D = 180 độ (AB//CD ; trong cùng phía)
=> góc A = 180 độ - 50 độ = 130 độ
Vậy góc A = 130 độ, góc B = 110 độ, góc C = 70 độ, D = 50 độ