Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo bài này nha!
Hình thang ABCD (AB//CD) có AC va BD cắt nhau tại O , AD và BC cắt nhau tại K . Chứng minh rằng OK đi qua trun?
Tứ giác ABCD là hình thang nên:AB//CD.
Gọi M, N lần lượt là giao điểm của KO với AB,CD.
Áp dụng định lý talet ta có:
AM/DN=MB/NC(=KM/KN)
=(AM+MB)/(CN+ND) (t/c dãy tỉ số bằng nhau) =AB/DC.
=AO/OC=AM/NC.
Vậy AM/DN=AM/NC hay DN=NC.
tương tự MB=MA.
hay ta có OK đi qua trung điểm của AB và CD.
: Tứ giác ABCD là hình thang nên:AB//CD.
Gọi M, N lần lượt là giao điểm của KO với AB,CD.
Áp dụng định lý talet ta có:
AM/DN=MB/NC(=KM/KN)
=(AM+MB)/(CN+ND) (t/c dãy tỉ số bằng nhau) =AB/DC.
=AO/OC=AM/NC.
Vậy AM/DN=AM/NC hay DN=NC.
tương tự MB=MA.
ta có OK đi qua trung điểm của AB và CD.

G A B M O N N' C D E F
Gọi \(N\) là trung điểm của đoạn thắng \(AB\) \(;\) \(N'\) là giao điểm của \(GM\) và \(AB\)
Tứ giác \(ABCD\) là hình thang nên \(AB\text{//}CD\)
Khi đó,
\(\Delta GMD\) có \(AN'\text{//}MD\), nên \(\frac{AN'}{MD}=\frac{GN'}{GM}\) (hệ quả của định lý Ta-lét) \(\left(3\right)\)
\(\Delta GMC\) có \(N'B\text{//}MC\), nên \(\frac{N'B}{MC}=\frac{GN'}{GM}\) \(\left(4\right)\)
\(\left(3\right);\) \(\left(4\right)\) \(\Rightarrow\) \(\frac{AN'}{MD}=\frac{N'B}{MC}\) \(\left(=\frac{GN'}{GM}\right)\)
Mà \(MD=MC\) \(\left(gt\right)\), do đó, \(AN'=N'B\) hay \(N'\) phải trùng với \(N\)
Tức là ba điểm \(G,\) \(N,\) \(M\) thẳng hàng \(\left(\text{*}\right)\)
Tương tự, ta cũng chứng minh được ba điểm \(N,\) \(O,\) \(M\) thẳng hàng \(\left(\text{**}\right)\)
Từ \(\left(\text{*}\right)\) và \(\left(\text{**}\right)\) suy ra bốn điểm \(G,\) \(N,\) \(O,\) \(M\) thẳng hàng
Vậy, đoạn thẳng \(GO\) sẽ lần lượt đi qua \(N\) và \(M\) hay đi qua trung điểm của \(AB\) và \(CD\)
Đặt AB = m, MC = MD = n.
a) Do AB // CD, ta có :
\(\frac{MI}{TA}=\frac{MD}{AB}=\frac{n}{m}\)
\(\frac{MK}{KB}=\frac{MC}{AB}=\frac{n}{m}\)
Từ (1) và (2) suy ra \(\frac{MI}{IA}=\frac{MK}{KB}\) Từ đó theo định lí đảo của định lí Ta - lét đối với tam giác MAB, ta có IK // AB. ( nhưng lớp 8 chưa học ta -lét thì fai )

Vì sử dụng kiến thức lớp 8 nên mik làm hơi dài. Nếu mik làm kiến thức lớp 9 là ra ngay thôi. Cảm ơn bạn, bài khá hay. Nếu bạn thấy hay thì like giúp mik nha. Thx bạn
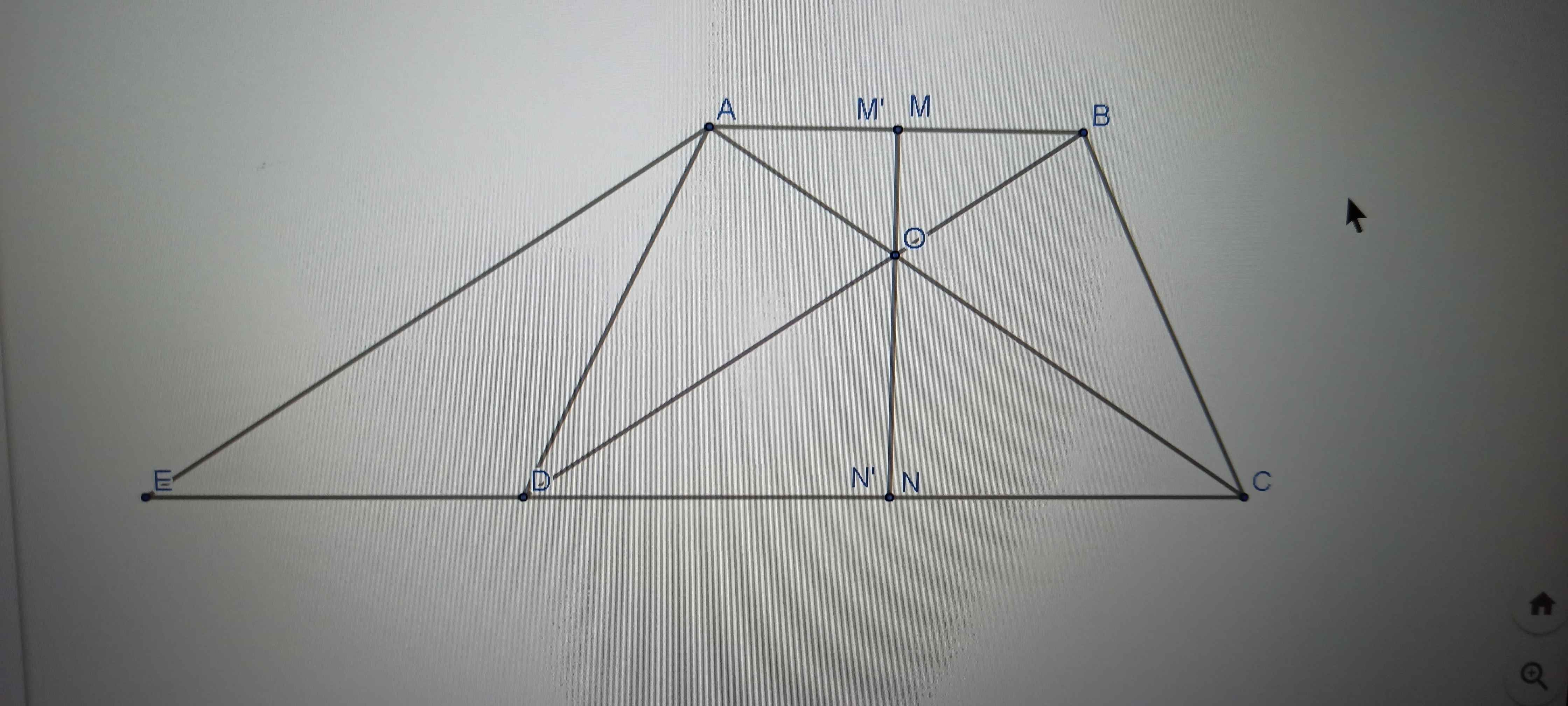


Xét ΔOAM và ΔOCN có
góc OAM=góc OCN
góc AOM=góc CON
=>ΔOAM đồng dạng vơi ΔOCN
=>AM/CN=OA/OC
Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
Do đó: ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD
Xét ΔOMB và ΔOND có
góc OMB=góc OND
góc MOB=góc NOD
=>ΔOMB đồng dạng vơi ΔOND
=>MB/ND=OB/OD=OA/OC=AM/NC
=>MB/MA=ND/NC=2
=>ND=2NC
=>CN/CD=1/3