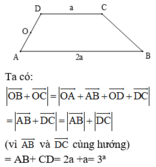
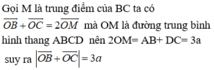Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hình thang ADCB có
Q,P lần lượt là trung điểm của AB,DC
=>QP là đường trung bình của hình thang ADCB
=>QP//AD//BC và \(QP=\dfrac{AD+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3}{4}BC\)
Ta có: M là trung điểm của BC
=>\(BM=MC=\dfrac{BC}{2}\)
Ta có: N là trung điểm của MC
=>\(MN=NC=\dfrac{MC}{2}=\dfrac{BC}{4}\)
BM+MN=BN
=>\(BN=\dfrac{1}{4}BC+\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
=>QP=BN
Ta có: QP//BN
QP=BN
Do đó: \(\overrightarrow{QP}=\overrightarrow{BN}\)
=>Điểm E trùng với điểm P

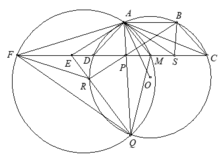
2). Vì EA là tiếp xúc (O) và từ kết quả câu 1) ta có E A 2 = E R . E Q = E P 2 .
Từ đó có E A = E P ⇒ D A P ^ = E A P ^ − E A D ^ = A P E ^ − A C D ^ = P A C ^
Do đó AP là phân giác D A C ^ ⇒ Q C = Q D ⇒ Q M ⊥ C D

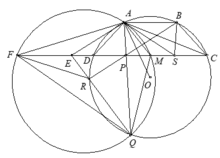
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.

Gọi M là trung điểm EF
\(\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{BE}+\dfrac{1}{2}\overrightarrow{BF}=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CF}\right)\)
\(=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}-\dfrac{1}{4}\overrightarrow{AB}=-\dfrac{7}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BM}=-\dfrac{7}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{DG}=\overrightarrow{DA}+\overrightarrow{AG}=-\overrightarrow{AD}+\overrightarrow{AG}=-\dfrac{1}{6}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AD}\)