Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


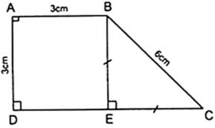
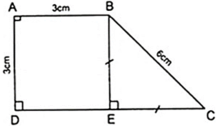
Kẻ BE ⊥ CD thì AD//BE do cùng vuông góc với CD
+ Hình thang ABED có cặp cạnh bên song song là hình bình hành.
Áp dụng tính chất của hình bình hành ta có
AD = BE = 3cm
Xét Δ BEC vuông tại E có 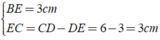
⇒ Δ BEC là tam giác vuông cân tại E.
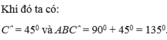

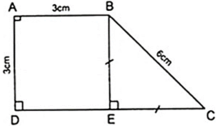
Kẻ BE ⊥ CD thì AD//BE do cùng vuông góc với CD
+ Hình thang ABED có cặp cạnh bên song song là hình bình hành.
Áp dụng tính chất của hình bình hành ta có
AD = BE = 3cm.
Xét Δ BEC vuông tại E có
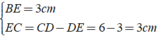
⇒ Δ BEC là tam giác vuông cân tại E.
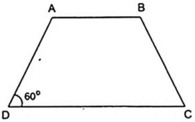
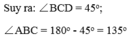

Xét hình thang cân ABCD ( AB//CD ) có Dˆ = 600
Theo định nghĩa và giả thiết về hình thang cân ta có: 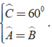
Do góc A và góc D là hai góc cùng nằm một phía của
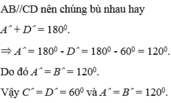

a) Hình thang ABCD có AB // CD
=> BAD + ADC = 180 độ
=> ADC = 90 độ
=> ABC + BCD = 180 độ
=> BCD = 90 độ

Bafi1: Do AB // CD ( GT )
⇒ˆA+ˆC=180o
⇒2ˆC+ˆC=180o
⇒3ˆC=180o
⇒ˆC=60o
⇒ˆA=60o.2=120o
Do ABCD là hình thang cân
⇒ˆC=ˆD
Mà ˆC=60o
⇒ˆD=60o
AB // CD ⇒ˆD+ˆB=180o
⇒ˆB=180o−60o=120o
Vậy ˆA=ˆB=120o;ˆC=ˆD=60o
Bài 2:
Ta có; AB//CD
\(\Rightarrow\)góc BAD+ góc ADC= \(180^o\)
^A=3. ^D \(\Rightarrow\)\(\dfrac{A}{3}\)=^D
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{A}{3}=\dfrac{D}{1}=\dfrac{A+D}{3+1}=\dfrac{180^O}{4}=45^O\)
\(\Rightarrow\)^A= \(135^O\)
\(\Rightarrow\)^D=\(45^o\)
\(\Rightarrow B=A=135^o\)
\(\Rightarrow C=D=45^o\)
gọi E là t/đ của DC.
do AB//CD nên ^A+^D=180 mà ^A=^D nên ^A=^D=90
xét tg ABED có : AB//ED(AB//DC, E thuộc DC): AB=AD ; DAB=90 => tg ABED là h.vuông (hơi tắt nhé!)
=>BE=EC(cùng= DE) và BE vg vs CE => tam giác BEc là tg vuông cân tại E=> C=45 và ^\(B_1\)=45
ta có:^B=\(B_1+B_2\)=45+90=135
- Cám ơn bạn nha. Tuy cách giải nó có hơi rắc rối nhưng mình hiểu á tks ^^