Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác ABCM có
D là trung điểm của đường chéo AC
D là trung điểm của đường chéo BM
Do đó: ABCM là hình bình hành
Suy ra: AM//BC và AM=BC(1)
Xét tứ giác ANBC có
E là trung điểm của đường chéo AB
E là trung điểm của đường chéo CN
Do đó: ANBC là hình bình hành
Suy ra: AN//BC và AN=BC(2)
Từ (1) và (2) suy ra AM=AN(3)
Ta có: AM//BC
AN//BC
mà AM và AN có điểm chung là A
nên N,A,M thẳng hàng(4)
Từ (3) và (4) suy ra A là trung điểm của NM

Lời giải:
Tam giác $ABC$ cân tại $A$ nên:
$\widehat{ABC}=\frac{180^0-\widehat{A}}{2}$
$M,N$ là trung điểm của $AB,AC$ mà $AB=AC$ nên $AM=AN$
$\Rightarrow \triangle AMN$ cân tại $A$
$\Rightarrow \widehat{AMN}=\frac{180^0-\widehat{A}}{2}$
Do đó: $\widehat{ABC}=\widehat{AMN}$
$\Rightarrow MN\parallel BC$
Trên tia đối của tia $NM$ lấy $P$ sao cho $NM=NP$
Dễ chứng minh $\triangle AMN=\triangle CPN$ (c.g.c)
$\Rightarrow \widehat{AMN}=\widehat{CPN}$ $\Rightarrow AM\parallel CP$
$\Rightarrow BM\parallel CP$
$\Rightarrow \widehat{BMC}=\widehat{PCM}$ (so le trong)
Xét tam giác $BMC$ và $PCM$ có:
$MC$ chung
$\widehat{BMC}=\widehat{PCM}$ (cmt)
$\widehat{BCM}=\widehat{PMC}$ (so le trong)
$\Rightarrow \triangle BMC=\triangle PCM$ (g.c.g)
$\Rightarrow BC=PM=2MN\Rightarrow MN=\frac{BC}{2}$


a) Xét △ABD và △ACE có:
AB = AC (gt)
\(\widehat{A}\) chung
AD = AE (gt)
\(\Rightarrow\)△ABD = △ACE (c.g.c)
\(\Rightarrow\)DB = EC (cặp cạnh tương ứng)
b) Ta có :△ABD = △ACE
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\) (cặp góc tương ứng)
Mà \(\widehat{ABC}=\widehat{ACB}\) ( △ABC cân tại đỉnh A)
\(\Rightarrow\widehat{ABC}-\widehat{B_1}=\widehat{ACB}-\widehat{C_1}\)
\(\Rightarrow\widehat{OBC}=\widehat{OCB}\)
\(\Rightarrow\)△OBC cân tại đỉnh O
\(\Rightarrow\)OB = OC
Ta có: DB = EC (cmt)
OB = OC
\(\Rightarrow\)DB - OB = EC - OC
\(\Rightarrow\)OE = OD
\(\Rightarrow\)△ODE cân đỉnh O (ĐPCM)
c) △OBC cân tại đỉnh O
\(\Rightarrow\)\(\widehat{OCB}=\frac{180^o-\widehat{BOC}}{2}\)
△ODE cân tại đỉnh O
\(\Rightarrow\widehat{DEO}=\frac{180^o-\widehat{DOE}}{2}\)
Mà \(\widehat{BOC}=\widehat{DOE}\)(đối đỉnh)
\(\Rightarrow\widehat{DEO}=\widehat{OCB}\)
Vì 2 góc này nằm ở vị trí so le trong
\(\Rightarrow\)DE // BC (ĐPCM)

Sửa câu c: DE // BE thành DE // BC nhé
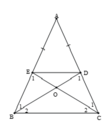
| GT | △ABC cân tại A. D BD ∩ ED = { O } |
KL | a, DB = EC b, △OBC cân; △ODE cân c, DE // BE |
Bài giải:
a, Vì △ABC cân tại A (gt) => AB = AC
Xét △BAD và △CAE
Có: AB = AC (cmt)
BAC là góc chung
AD = AE (gt)
=> △BAD = △CAE (c.g.c)
=> DB = CE (2 cạnh tương ứng)
b, Vì △BAD = △CAE (cmt)
=> ABD = ACE (2 góc tương ứng) và ADB = CEA (2 góc tương ứng)
Ta có: CEA + CEB = 180o (2 góc kề bù)
ADB + BDC = 180o (2 góc kề bù)
Mà ADB = CEA (cmt)
=> CEB = BDC
Lại có: AB = AE + EB
AC = AD + DC
Mà AB = AC (gt) ; AD = AE (gt)
=> EB = DC
Xét △BOE và △COD
Có: OBE = OCD (cmt)
BE = CD (cmt)
BEO = CDO (cmt)
=> △BOE = △COD (g.c.g)
=> OB = OC (2 cạnh tương ứng) và OE = OD (2 cạnh tương ứng)
Xét △OED có: OE = OD (cmt) => △OED cân tại O
Xét △OBC có: OB = OC (cmt) => △OBC cân tại O
c, Xét △AOD có: AE = AD (gt) => △AOD cân tại A => AED = (180o - EAD) : 2 (1)
Vì △ABC cân tại A (gt) => ABC = (180o - BAC) : 2 (2)
Từ (1) và (2) => AED = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> ED // BC (dhnb)

a) Xét ΔABD và ΔACE có:
AB=ACAB=AC (do ΔABC cân đỉnh A)
ˆA^ : góc chung
AD=AE (giả thiết)
⇒ΔABD=ΔACE (c.g.c)
⇒DB=EC (hai cạnh tương ứng)
b) ΔABD=ΔACE⇒ˆB1=ˆC1 (hai góc tương ứng)
Mà ˆABC=ˆACB (do ΔABC cân đỉnh A)
⇒ˆABC−ˆB1=ˆACB−ˆC1
⇒ˆOBC=ˆOCB
⇒ΔOBC cân đỉnh O (đpcm)


 AC; E
AC; E
Bạn tự vẽ hình nha
Ta có:AB = AC ( △ABC cân tại A )
Mà AE = EB ( E là trung điểm của AB)
AD = ED ( D là trung điểm của AC)
Nên AE = ED
Xét △ABD và △ACE có
AB = AC ( △ ABC cân tại A )
A là góc chung
AE = ED ( cmt )
Vậy △ABD = △ACE ( c - g - c )
➩ DB = EC ( 2 cạnh tương ứng )
Có E,D lần lượt là trung điểm của AB ; AC
Mà AB = AC
=> AE = AD
Xét t/g ABD và t/g ACE có
AB = AC
\(\widehat{A}\) : chung
AD = AE
=> t/g ABD = t/g ACE
=> BD = CE