Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
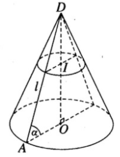
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với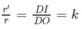 
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
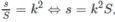
trong đó S = πr 2 = πl 2 cos 2 α
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s = k 2 s = k 2 πl 2 cos 2 α
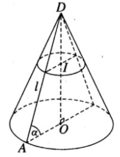
Gọi r là bán kính của đường tròn đáy.
Ta có OA = r = l.cos α (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).
Ta suy ra: S xq = πrl = πl 2 cosα
Khối nón có chiều cao h = DO = lsin α . Do đó thể tích V của khối nón được tính theo công thức
Vậy :
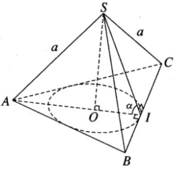
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và
Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy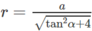 
Hình nón nội tiếp có đường sinh là :
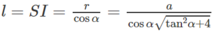
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
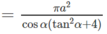
Đáp án A
Giả sử thiết diện là một tam giác cân có độ dài chiều cao hạ từ đỉnh nón xuống đáy tam giác là x ( 0 < x < R 2 + h 2 )
Khi đó ta dễ dàng tính được độ dài đáy tam giác theo x, h và R là:
2 R 2 + h 2 - x 2
Do đó, diện tích S của tam giác là:
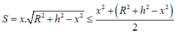(BĐT Cauchy)
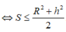
Vậy S m a x = R 2 + h 2 2
