Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

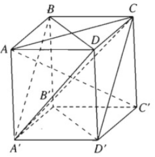
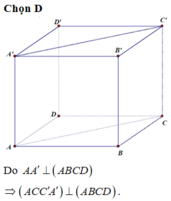
a) Ta có AB = AD = AA′ = a
và C ′ B = C ′ D = C ′ A ′ = a 2
Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)
b) Ta có ACC’ là tam giác vuông có cạnh A C = a 2 và CC’ = a
Vậy A C ′ 2 = A C 2 + C C ′ 2
⇒ A C ′ 2 = 2 a 2 + a 2 = 3 a 2 . V ậ y A C ′ = a 3 .

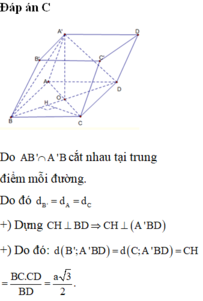
Ta có: BD = A’B = A’D nên tam giác A’BD là tam giác đều.
Lại có: AB = AD = AA’ nên hình chiếu vuông góc của điểm A lên mp(A’BD) là tâm của tam giác BDA’.
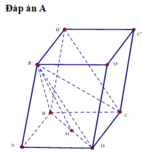
Đáp án D

Gọi M là trung điểm của BD, là trung điểm của A’B.
Suy ra tâm O của tam giác BDA’ là giao của DN và A’M
Phương án D đúng vì BD ⊥ (AMA') bởi BD ⊥ AM và BD ⊥ A’M ⇒ BD ⊥ AO
BA’ ⊥ (AND) do BA’ ⊥ DN và A’B ⊥ AN ⇒ A’B ⊥ AO
AO ⊥ (A’BD) ⇒ O là hình chiếu của A trên (A’BD).
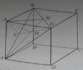
Đáp án D


b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)
Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)
Vậy \(AC'=a\sqrt{3}\)

Đáp án B
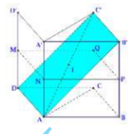
Gọi M, N, P, Q lần lượt là trung điểm của BB’, AA’, DD’, CC’
Khi đó mặt phẳng (P) thỏa yêu cầu bài toán chính là mặt phẳng (MNPQ)
Qua phép đối xứng của mặt phẳng (P) thì tứ giác ADC'B' biến thành A'D'CB
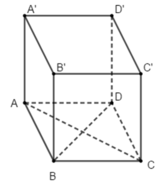
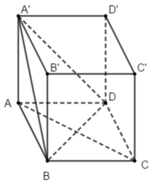
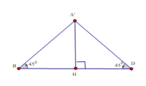
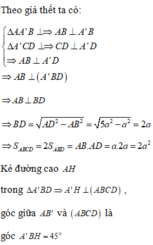

Ta có: B D ⊥ A C B D ⊥ A A ' ⇒ B D ⊥ ( A C C ' A ' )
* Vì B D ⊂ ( A B C D ) ⇒ ( A B C D ) ⊥ ( A C C ' A ' )
* Vì B D ⊂ ( B D C ' ) ⇒ ( B D C ' ) ⊥ ( A C C ' A ' )
* Vì B D ⊂ ( A ' B D ) ⇒ ( A ' B D ) ⊥ ( A C C ' A ' )
Vậy mp(CDD’C’) không vuông góc với mặt phẳng (ACC’A’).
Chọn B.