Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
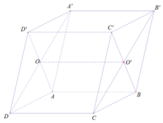
Ta có: C’B ∩ CB’ = O '
⇒ O’ là điểm chung của (A’B’CD) và (ABC’D’)
A’D ∩ AD’ = O
⇒ O là điểm chung của (A’B’CD) và (ABC’D’)
⇒ OO’ là giao tuyến cần tìm

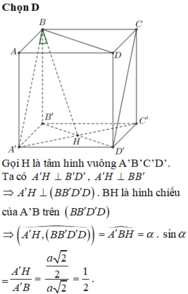
Đáp án D
Ta chứng minh (AB’D’)//(BC’D)
Khi đó d((AB’D’), (BC’D))=d(C,(BC’D))
Ta chứng minh (BC’D)⊥(ACC’). Rồi từ C kẻ CH ⊥ OC’suy ra CH ⊥(BC’D)
Ta có ![]()
![]()

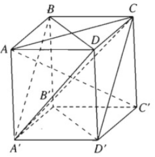
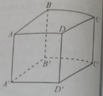
a) Ta có AB = AD = AA′ = a
và C ′ B = C ′ D = C ′ A ′ = a 2
Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)
b) Ta có ACC’ là tam giác vuông có cạnh A C = a 2 và CC’ = a
Vậy A C ′ 2 = A C 2 + C C ′ 2
⇒ A C ′ 2 = 2 a 2 + a 2 = 3 a 2 . V ậ y A C ′ = a 3 .

Vì CD // C’D’ nên góc giữa AC và C’D’ bằng góc giữa AC và CD – bằng góc ACD
Vì ABCD là hình vuông nên tam giác ACD vuông cân tại D
⇒ A C D ^ = 45 0
Đáp án B
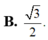
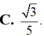
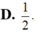

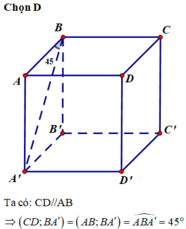
ĐÁP ÁN: D