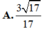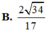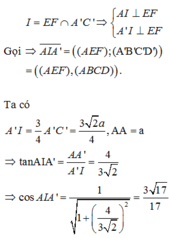Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

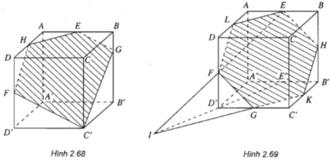
Ta xác định thiết diện của hình lập phương cắt bởi các mặt phẳng sau:
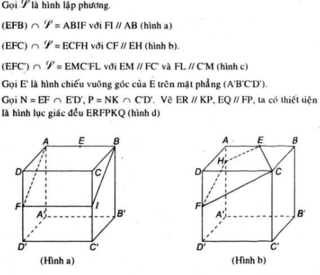
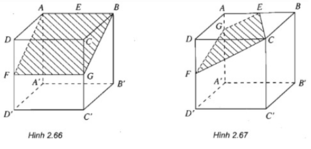
- Mặt phẳng (EFB): ta vẽ FG //AB và được thiết diện là hình chữ nhật ABGF, G là trung điểm của CC'.
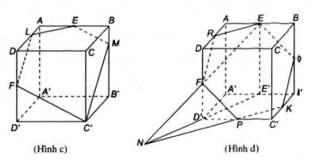
- (h.2.67) Mặt phẳng (EFC): Nối FC và vẽ EG // FC, ta được thiết diện là hình thang ECFG
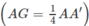
- (h.2.68) Mặt phẳng (EFC'): Nối FC' và vẽ EG // FC′. Nối GC' và vẽ FH // GC′. Ta được thiết diện là hình ngũ giác EGC'FH.
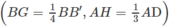
- (h.2.69) Mặt phẳng (EFK) với K là trung điểm của đoạn B'C'. Lấy trung điểm E' của đoạn A'B'. Ta có I = EF ∩ E′D. Ta có IK là giao tuyến của hai mặt phẳng (EFK) và (A'B'C'D'). Gọi G = IK ∩ C′D′. Nối F với G, vẽ EH // FG. Nối K với H, vẽ FL // KH và nối L với E. Ta được thiết diện là hình lục giác đều EHKGFL. (G, H, L theo thứ tự là trung điểm của D'C', B'B, AD).

a: ABCD.A'B'C'D' là hình lập phương
=>AA'//BB'//CC'//DD' và AA'=BB'=CC'=DD'
Xét tứ giác AA'C'C có
AA'//CC'
AA'=CC'
Do đó: AA'C'C là hình bình hành
=>AC//A'C'
ABCD.A'B'C'D' là hình lập phương
=>ABCD và A'B'C'D' là hình vuông
ABCD là hình vuông
=>AC là phân giác của góc BAD và CA là phân giác của góc BCD
=>\(\widehat{BAC}=\widehat{DAC}=45^0\) và \(\widehat{BCA}=\widehat{DCA}=45^0\)
\(\widehat{A'C';BC}=\widehat{AC;BC}=\widehat{ACB}=45^0\)
b: Xét ΔBAC có M,N lần lượt là trung điểm của BC,BA
=>MN là đường trung bình của ΔBAC
=>MN//AC
Xét ΔA'AD' có
E,F lần lượt là trung điểm của AA',A'D'
=>EF là đường trung bình của ΔA'AD'
=>EF//AD'
ABCD.A'B'C'D là hình vuông
=>ADD'A' là hình vuông; DCC'D' là hình vuông
ABCD là hình vuông
=>\(AC=AB\cdot\sqrt{2}\)(1)
ADD'A' là hình vuông
=>\(AD'=AD\cdot\sqrt{2}=AB\cdot\sqrt{2}\)(2)
DCC'D' là hình vuông
=>\(CD'=CD\cdot\sqrt{2}=AB\cdot\sqrt{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AC=AD'=D'C
=>ΔAD'C đều
=>\(\widehat{D'AC}=60^0\)
\(\widehat{MN;EF}=\widehat{AC;AD'}=\widehat{CAD'}=60^0\)
c: \(\widehat{MN;BC}=\widehat{AC;CB}=\widehat{ACB}=45^0\)
d: \(\widehat{EF;CC'}=\widehat{AD';DD'}=\widehat{AD'D}=45^0\)