Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
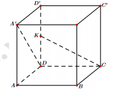
Chọn hệ trục với D 0 ; 0 ; 0 , A a ; 0 ; 0 , A ' a ; 0 ; a , K 0 ; 0 ; a 2 , C 0 ; a ; 0
Khi đó D A ' → = a ; 0 ; a , K C → 0 ; a ; - a 2 ⇒ D A ' → ; K C → = a 2 2 2 ; - 1 ; - 2
Phương trình mặt phẳng qua C (chứa CK) và song song với DA’ là (P):2x - y - 2z + a = 0
Khi đó d C K ; A ' D = d D ; P = a 3 .
Đáp án D.
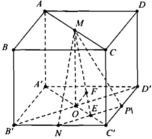
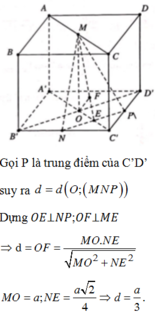
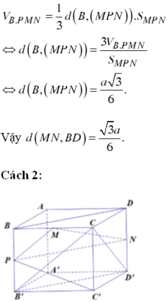
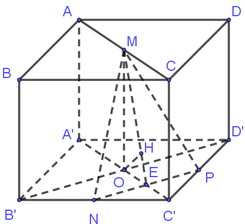
Gọi P là trung điểm của C’D’ suy ra d = d O ; M N P
Dựng:
O A ⊥ N P ; OF ⊥ ME ⇒ d=OF= M O . N E M O 2 + N E 2
trong đó
M O = a ; N E = a 2 4 ⇒ d = a 3 .
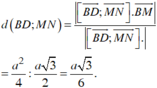
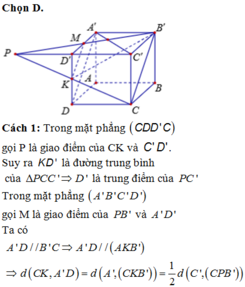
Đáp án A
Phương pháp:
- Sử dụng phương pháp tọa độ hóa.
- Công thức tính khoảng cách giữa hai đường thẳng chéo nhau:
Cho ∆ có VTCP u → và qua M; ∆ ' có VTCP v → và qua M’
Cách giải:
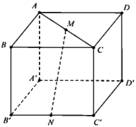
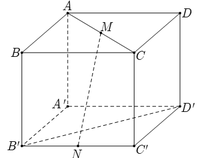
Gắn hệ trục tọa độ như hình vẽ, trong đó:
A'(0;0;0), B'(0;a;0), C'(a;a;0), D'(a;0;0)
A(0;0;a), B(0;a;a), C(a;a;a); D(a;0;a), M(a/2;a;a)
Đường thẳng AM có VTCP
và qua A(0;0;a)
Đường thẳng DB’ có VTCP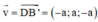
và qua D(a;0;a)
A D → = ( a ; 0 ; 0 )
Khoảng cách giữa hai đường thẳng AM và DB’: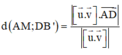
Ta có:
Vây, khoảng cách giữa AM và DB’ là a 2 7