Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

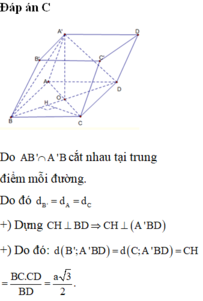
Gọi M là trung điểm của BD, là trung điểm của A’B.
Suy ra tâm O của tam giác BDA’ là giao của DN và A’M
Phương án D đúng vì BD ⊥ (AMA') bởi BD ⊥ AM và BD ⊥ A’M ⇒ BD ⊥ AO
BA’ ⊥ (AND) do BA’ ⊥ DN và A’B ⊥ AN ⇒ A’B ⊥ AO
AO ⊥ (A’BD) ⇒ O là hình chiếu của A trên (A’BD).
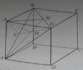
Đáp án D

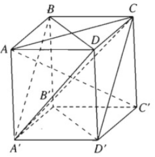
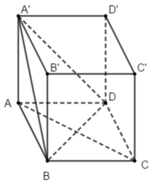
a) Ta có AB = AD = AA′ = a
và C ′ B = C ′ D = C ′ A ′ = a 2
Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)
b) Ta có ACC’ là tam giác vuông có cạnh A C = a 2 và CC’ = a
Vậy A C ′ 2 = A C 2 + C C ′ 2
⇒ A C ′ 2 = 2 a 2 + a 2 = 3 a 2 . V ậ y A C ′ = a 3 .

Phương án A sai vì AC không vuông góc với CD ⊂ (CDD’C’)
Phương án B sai vì AC // (A’B’C’D’)
Phương án C đúng vì AC ⊥ BD , AC⊥ BB’ và BD, BB’ ⊂ (BDD’B’)
Đáp án C

Ta có: BD = A’B = A’D nên tam giác A’BD là tam giác đều.
Lại có: AB = AD = AA’ nên hình chiếu vuông góc của điểm A lên mp(A’BD) là tâm của tam giác BDA’.
Đáp án D

THAM KHẢO:

a) Vì AA′⊥(ABCD) nên góc giữa đường thẳng AA' và (ABCD) là \(90^0\)
b) CC′⊥(ABCD) nên C là hình chiếu vuông góc của C' lên (ABCD).
Suy ra góc giữa BC' và (ABCD) là \(\widehat{C'BC}\)=\(45^O\) (Vì BCC'C' là hình vuông)c) Gọi cạnh của hình lập phương là a
Ta có: AC=\(a\sqrt{2}\),tan \(\widehat{ACA'}\)=\(\dfrac{1}{\sqrt{2}}\) nên \(\widehat{ACA'}\)=\(35^O\)
AA′⊥(ABCD) nên A là hình chiếu vuông góc của A' lên (ABCD)
Suy ra góc giữa A'C và (ABCD) là \(\widehat{ACA'}\)=\(35^O\)


b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)
Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)
Vậy \(AC'=a\sqrt{3}\)

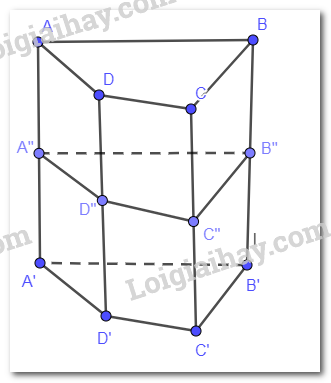
Mặt phẳng (ABCD) song song với (A"B"C"D") (do cùng song song với (A'B'C'D')) nên ABCD.A"B"C"D" là hình lăng trụ tứ giác.
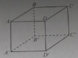

Đáp án B