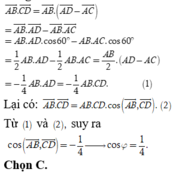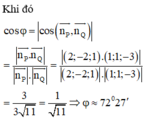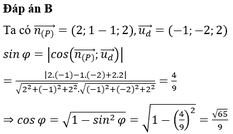Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
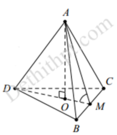
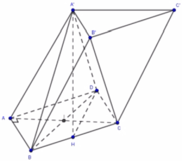
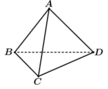
Gọi M là trung điểm của
B C ⇒ A M ⊥ B C D M ⊥ B C ⇒ B C ⊥ A D M
Suy ra
A B C ; D B C ^ = A M ; D M ^ = A D M ^ = φ
Gọi O là hình chiếu của A lên
mặt phẳng B C D
⇒ O là trọng tâm của tam giác BCD
⇒ O M = D M 3 = 1 3 . a 3 2 = a 3 6
Tam giác AMO vuông tại O, có
cos A M D ^ = O M A M = a 3 6 : a 3 2 = 1 3
Vậy cos φ = 1 3

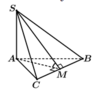
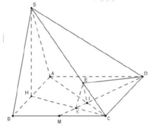
Gọi M là trung điểm BC, suy ra A M ⊥ B C
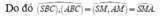
Tam giác ABC đều cạnh a suy ra trung tuyến ![]()
Tam giác vuông SAM có ![]()
Chọn D.

Đáp án B.
Phương pháp:
Sử dụng công thức Côsin:
a 2 = b 2 + c 2 − 2 b c cos A
Cách giải:
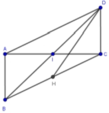
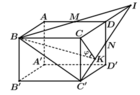
Dựng hình bình hành ABCD (tâm I). Khi đó, A’B’CD là hình bình hành (do A ' B ' → = A B → = D C → )
⇒ A ' D / / B ' C ⇒ A ' B ; B ' C = A ' B ; A ' D
Tam giác ABC vuông tại A
⇒ B C = A B 2 + A C 2 = a 2 + a 3 2 = 2 a
H là trung điểm của BC
⇒ H B = H C = a
Tam giác A’BH vuông tại H
⇒ A ' B = A ' H 2 + H B 2 = a 3 2 + a 2 = 2 a
Tam giác ABC vuông tại A
⇒ cos A B C = A B B C = a 2 a = 1 2
ABCD là hình bình hành
⇒ A B / / C D ⇒ D C B = 180 0 − A B C ⇒ cos D C B = − c osABC=- 1 2
Tam giác BCD:
B D = B C 2 + C D 2 − 2 B C . C D . cos D C B = 2 a 2 + a 2 − 2.2 a . a . − 1 2 = a 7
Tam giác CDH:
D H = C H 2 + C D 2 − 2 C H . C D . cos D C B = a 2 + a 2 − 2 a . a . − 1 2 = a 3
Tam giác A’DH vuông tại H:
A ' D = A ' H 2 + H D 2 = a 3 2 + a 3 2 = a 6
Tam giác A’BH:
cosBA ' D = A ' D 2 + A ' B 2 − B D 2 2 A ' D . A ' B = a 6 2 + 2 a 2 − 7 a 2 2. a 6 .2 a = 3 4 6 = 6 8 .