Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

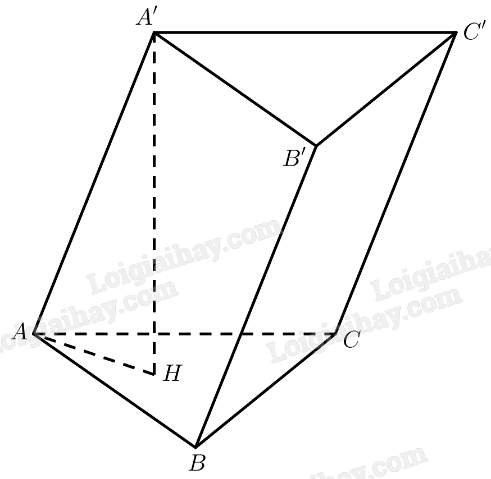
Gọi \(H\) là hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\)
\(\begin{array}{l} \Rightarrow A'H \bot \left( {ABC} \right)\\ \Rightarrow \left( {AA',\left( {ABC} \right)} \right) = \left( {AA',AH} \right) = \widehat {A'AH}\end{array}\)
\(\Delta AA'H\) vuông tại \(H \Rightarrow A'H = AA'.\sin \widehat {A'AH} = \frac{{a\sqrt 3 }}{2}\)
Vì \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\) nên \(d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = d\left( {A',\left( {ABC} \right)} \right) = A'H = \frac{{a\sqrt 3 }}{2}\)

Đáp án D.
Gọi M là trung điểm BC, dựng ![]()
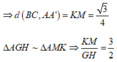
![]()
∆ AA'G vuông tại G, GH là đường cao => A'G = 1 3
Vậy 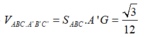

Đáp án C
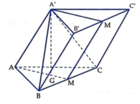
Ta dễ dàng chứng minh được AA'//(BCC'B')
![]()
![]()
Gọi G là trọng tâm của tam giác ABC. Suy ra A'G ⊥ (ABC)
Ta có
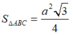
![]()
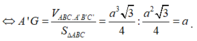
Lại có
![]()
![]()
Ta luôn có
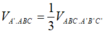
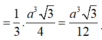
![]()
![]()

Gọi M, M' lần lượt là trung điểm của BC và B'C'. Ta có ![]() .
.![]()
Mà MM'//BB' nên BC ⊥ BB' => BCC'B' là hình chữ nhật
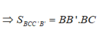
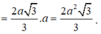
Từ:
![]()
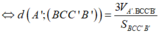
![]()
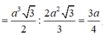
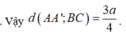

Kẻ \(CH\perp AB\Rightarrow AB\perp\left(CC'H\right)\)
\(\Rightarrow\widehat{CHC'}\) là góc giữa (C'AB) và (ABC) \(\Rightarrow\widehat{CHC'}=30^0\)
\(\Rightarrow CH=C'H.cos30^0=\dfrac{C'H.\sqrt{3}}{2}\)
\(S_{ABC}=\dfrac{1}{2}CH.AB=\dfrac{\sqrt{3}}{2}.\left(\dfrac{1}{2}C'H.AB\right)=\dfrac{\sqrt{3}}{2}S_{C'AB}=6\sqrt{3}\)
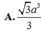

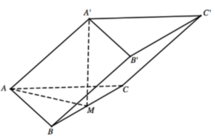

a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)