Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

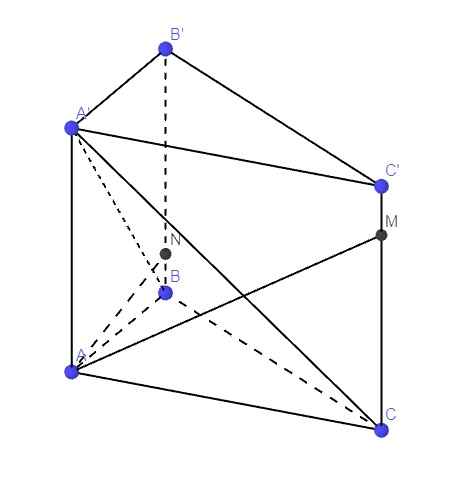
Chắc đề đúng là tính \(d\left(A;\left(BCC'B'\right)\right)\)
Gọi E là trung điểm BC \(\Rightarrow AE\perp BC\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AE\perp\left(BCC'B'\right)\)
\(\Rightarrow AE=d\left(A;\left(BCC'B'\right)\right)\)
Ta có: \(AE=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(\Rightarrow d\left(A;\left(BCC'B'\right)\right)=\dfrac{a\sqrt{3}}{2}\)

a.
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)

\(\widehat{A'BA}=60^0\Rightarrow AA'=AB.tan60^0=a\sqrt{3}\)
(Lại 1 bài mà sử dụng tọa độ hóa sẽ cho kết quả cực kì nhanh chóng).
Lớp 11 thì chắc phải dựng hình:
Trong mp (A'B'C'), qua C' kẻ đường thẳng song song A'B', qua B' kẻ đường thẳng song song A'C', hai đường thẳng này cắt nhau tại D'
\(\Rightarrow AC'||BD'\) (do tứ giác ABD'C' là hình bình hành)
\(\Rightarrow d\left(AC';A'B\right)=d\left(AC';\left(A'BD'\right)\right)=d\left(C';\left(A'BD'\right)\right)\)
Gọi giao điểm của A'D' và B'D' là O \(\Rightarrow OB'=OC'\) theo t/c 2 đường chéo hbh
\(\Rightarrow d\left(C';\left(A'BD'\right)\right)=d\left(B';\left(A'BD'\right)\right)\)
Quy được về 1 bài tính khoảng cách cơ bản: tứ diện B.A'B'D' có \(BB'\perp\left(A'B'D'\right)\) , tìm k/c từ B' đến mp (A'BD')
Lần lượt kẻ B'H vuông góc A'D' và B'K vuông góc BH thì B'K là k/c cần tìm
Bạn tự tính toán nốt nhé