Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

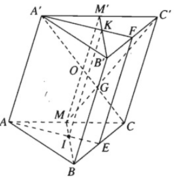
Gọi M và M’ tương ứng là trung điểm của AC và A’C’, ta có:
I ∈ BM, G ∈ C′M, K ∈ B′M′
Theo tính chất trọng tâm của tam giác ta có:
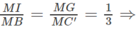
Ta có :
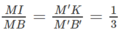
Mặt khác IG và IK ⊂ (IGK) nên (IGK) // (BB′C′C)
b) Gọi E và F tương ứng là trung điểm của BC và B’C’, O là trung điểm của A’C. A, I, E thẳng hàng nên (AIB’) chính là (AEB’). A’, G, C thẳng hàng nên (A’GK) chính là (A’CF).
Ta có B′E // CF (do B’FCE là hình bình hành ) và AE // A′F nên (AIB′) // (A′GK).

Ta có: ABB'A' là hình bình hành, M, N là trung điểm của AA', BB' nên MN // AB (đường trung bình) suy ra MN // (ABC).
Tương tự, ta có NP // BC suy ra NP// (ABC).
Mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN, NP và MN, NP song song với mp(ABC) suy ra (MNP) //(ABC).

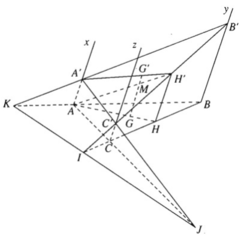
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
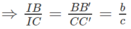
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
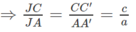
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
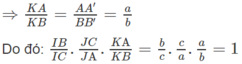
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
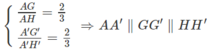
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
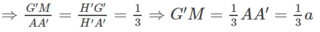
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
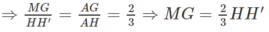
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
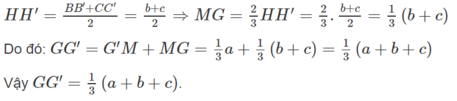

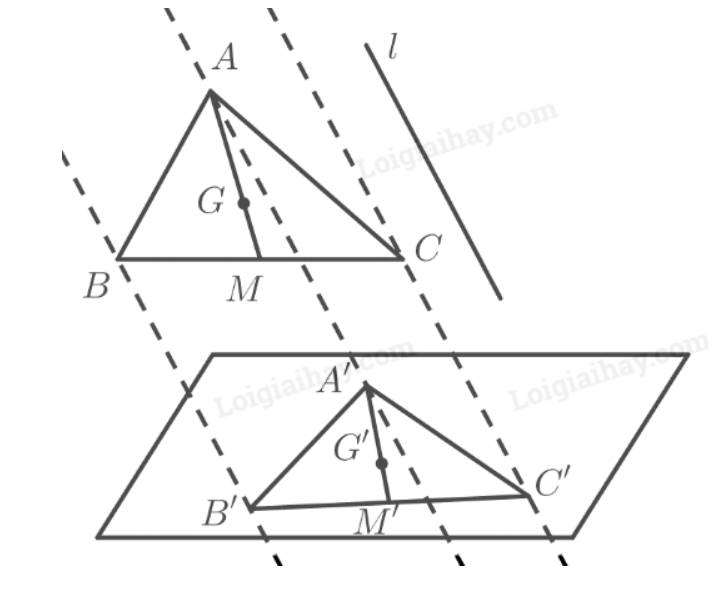
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(M\) nằm giữa \(B\) và \(C\) thì \(M'\) nằm giữa \(B'\) và \(C'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(MB = MC\) thì \(M'B' = M'C'\).
Vậy \(M'\) là trung điểm của \(B'C'\).
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(G\) nằm giữa \(A\) và \(M\) thì \(G'\) nằm giữa \(A'\) và \(M'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(AG = \frac{2}{3}AM\) thì \(A'G' = \frac{2}{3}A'M'\).
Vậy \(G'\) là trọng tâm tam giác \(A'B'C'\).




Qua G kẻ đường thẳng song song BC cắt AC tại E
\(\Rightarrow E\in\left(P\right)\) và \(\frac{AE}{AC}=\frac{2}{3}\) (theo Talet và t/c trọng tâm)
Trong mặt phẳng (ACC'A'), qua E kẻ đường thẳng song song A'C cắt CC' và AA' lần lượt tại M và N
\(\Rightarrow\frac{CM}{AN}=\frac{EC}{AE}=\frac{1}{2}\Rightarrow CM=\frac{1}{2}AN\) (Talet)
Cũng theo Talet: \(\frac{AN}{AA'}=\frac{AE}{AC}=\frac{2}{3}\Rightarrow AN=\frac{2}{3}AA'=\frac{2}{3}CC'\)
\(\Rightarrow CM=\frac{1}{2}.\frac{2}{3}CC'\Rightarrow\frac{CM}{CC'}=\frac{1}{3}\)