Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\Rightarrow AM\perp\left(BCC'B'\right)\)
\(\Rightarrow\widehat{AC'M}\) là góc giữa AC' và (BCC'B')
\(AM=\dfrac{a\sqrt{3}}{2}\) ; \(C'M=\sqrt{C'C^2+\left(\dfrac{BC}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}\)
\(tan\widehat{AC'M}=\dfrac{AM}{C'M}=\dfrac{\sqrt{15}}{5}\)

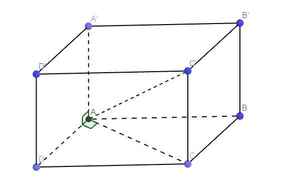
Do \(\left\{{}\begin{matrix}AA'\perp\left(ABCD\right)\Rightarrow AA'\perp AD\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(AA'C\right)\)
Mà \(AD||A'D'\Rightarrow A'D'\perp\left(AA'C\right)\)
Lại có \(AA'||CC'\Rightarrow C'\in\left(AA'C\right)\Rightarrow A'D'\perp AC'\) (1)
\(\left\{{}\begin{matrix}AA'\perp AC\\AA'=AC\end{matrix}\right.\) \(\Rightarrow\) tứ giác AA'C'C là hình vuông
\(\Rightarrow AC'\perp A'C\) (2)
(1);(2) \(\Rightarrow AC'\perp\left(A'D'C\right)\)

Gọi M là trung điểm BC \(\Rightarrow MG\) là đường trung bình tam giác BCB'
\(\Rightarrow MG||BB'\Rightarrow MG\perp\left(ABC\right)\)
\(\Rightarrow\widehat{GAM}\) là góc giữa AG và (ABC)
\(MG=\dfrac{1}{2}BB'=\dfrac{a}{2}\) ; \(AM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
\(tan\widehat{GAM}=\dfrac{MG}{AM}=\dfrac{\sqrt{3}}{3}\)

Tam giác \(ABC\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}} = a\sqrt 3 \)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AC\)
\( \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow A'C = \sqrt {AA{'^2} + A{C^2}} = \sqrt {{h^2} + 3{{\rm{a}}^2}} \).
Gọi \(O\) là tâm lục giác đều \(ABC{\rm{DEF}}\).
\(\Delta OAB,\Delta OC{\rm{D}}\) đều \( \Rightarrow OA = O{\rm{D}} = AB = a \Rightarrow A{\rm{D}} = 2a\)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AD\)
\( \Rightarrow \Delta AA'D\) vuông tại \(A\)
\( \Rightarrow A'D = \sqrt {AA{'^2} + A{D^2}} = \sqrt {{h^2} + 4{{\rm{a}}^2}} \).