Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

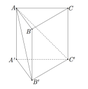
Đáp án D.
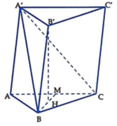
Gọi H là trọng tâm của tam giác ABC, từ giả thiết suy ra B ' H ⊥ A B C .
Khi đó
B B ' , A B C ^ = B B ' , B H ^ = B ' B H ^ = 60 °
Ta có
B B ' = a ⇒ B H = B B ' . cos B ' B H ^ = a . cos 60 ° = a 2 , B ' H = B ' B 2 − B H 2 = a 3 2
Gọi M là trung điểm BC, suy ra B H = 2 3 B M ⇒ B M = 3 2 B H = 3 2 . a 2 = 3 a 4 .
Đặt A C = x > 0 ⇒ B C = A C . tan B A C ^ = x . tan 60 ° = x 3 ⇒ A B = A B 2 + A C 2 = 2 x .
Lại có
B M = B C 2 + C M 2 = B C 2 + A C 2 4 = 3 x 2 + x 2 4 = x 13 2 = 3 a 4 ⇒ x = 3 a 2 13
⇒ A C = 3 a 2 13 , B C = 3 3 a 2 13 , A B = 6 a 2 13 ⇒ S Δ A B C = 1 2 A C . B C = 9 3 a 2 104
(đvdt).
Vậy V A ' A B C = 1 3 B ' H . S Δ A B C = 1 3 . a 3 2 . 9 3 a 2 104 = 9 a 3 208 (đvtt).

Đáp án B
Gọi M, N lần lượt là trung điểm của AC và AM.
Khi đó ΔAHM là tam giác đều và NH ⊥ AC .



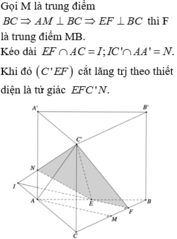
Đáp án D
Phương pháp :
+) Kẻ AD ⊥ B’C, xác định góc giữa mặt phẳng (AB’C) và mặt phẳng (BCC’B’)
+) Tính BB’.
+) Tính thể tích khối lăng trụ và suy ra thế tích AB’CA’C’
Cách giải :
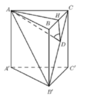
Gọi H là trung điểm của BC ta có
![]()
Trong (AB’C) kẻ AD ⊥ B’C
![]()
Ta có:

=> ((AB'C);(BCC'B')) = (AD;HD) = ADH
Ta có 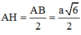

Dễ thấy ∆CBB’ đồng dạng với ∆CDH (g.g)
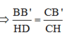
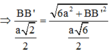
![]()
![]()
Ta có: 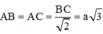
![]()
![]()
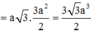
![]()
![]()

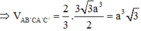

Chọn D.
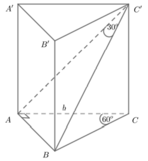
Phương pháp : Xác định góc. Diện tích xung quanh hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao. Từ đó xác định chu vi đáy và chiều cao.

Vậy diện tích xung quanh hình lăng trụ là
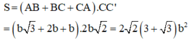
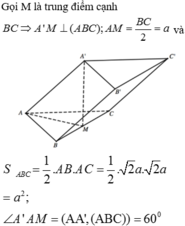
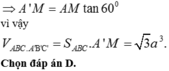
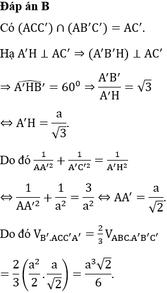
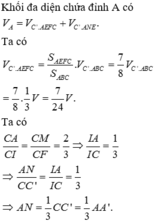
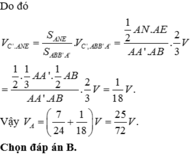
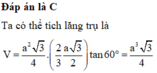

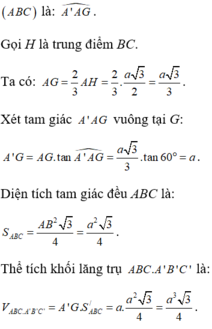
Đáp án A