Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
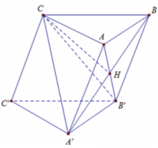
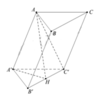
Gọi H là tâm của hình bình hành ABB'A'.
Khi đó C H ⊥ A B B ' A ' .
Do H là tâm của hình bình hành nên các tam giác C A ’ B ; C A B ’
là các tam giác cân tại C ( Do trung tuyến đồng thời là đường cao).
Khi đó C B = C A ' = a ; C A = C B ' = a . Suy ra C C ’ A ’ B ’ là tứ diện đều cạnh a. Tính nhanh ta có:
V C . C ' A ' B ' = a 3 2 12 ⇒ V A B C . A ' B ' C ' = a 3 2 4 .
Đáp án A
Khoảng cách giữa hai mặt đáy là h = AH = A’H.tan A A ' H ^ = a 3 2 . tan 30 0 = a 2
Đáp án B
Phương pháp giải:
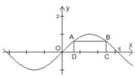
Dựa vào đồ thị hàm số xác định hoành độ điểm D suy ra tung độ điểm A chính là độ dài BC
Lời giải: Gọi 
với 
Gọi 
thuộc đồ thị 
Vì ABCDlà hình chữ nhật 
Khi đó BC = m. Mà 
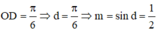
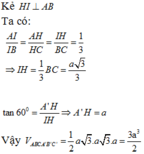
Đáp án A
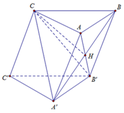
Gọi O là tâm hình bình hành A B B ' A ' , ta có C O ⊥ A B B ' A ' .
Vì C A = C B nên O A = O B , suy ra hình thoi A B B ' A ' là hình vuông.
Do đó O A = A B 2 = a 2 . Suy ra O C 2 = A C 2 − A O 2 = a 2 2 ⇒ O C = a 2
Suy ra tam giác ABC vuông tại C. Từ đây ra suy ra khối caauff đi qua năm điểm A ; B ; B ' ; A ' và C là khối cầu tâm O bán kính O A = a 2 .
Vậy thể tích khối cầu là V = 4 3 π . O A 3 = π 2 a 3 3