Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


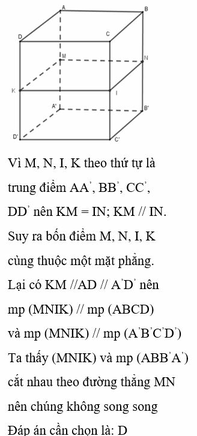
a) BB’ ⊥ A’B’ (ABB’A’ là hình chữ nhật)
BB’ ⊥ B’C’ (BCC’B’ là hình chữ nhật)
=> BB’ ⊥ mp(A’B’C’D’)
=> BB’ ⊥ B’D’ hay
Hình bình hành BDD’B’ có một góc vuông nên là hình chữ nhật
BB’ vuông góc với hai đường thẳng cắt nhau AB và BC
=> BB’ ⊥ mp(ABCD)
c) mp(ABB’A’) chứa BB’ mà BB’⊥ mp(ABCD)
=> mp(ABB’A’) ⊥ mp(ABCD)

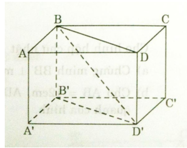
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)

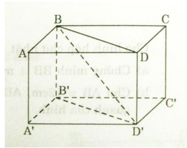
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)

Ta có : \(AA'//CC'\left(cùng//BB'\right)\)
\(\Rightarrow AM//C'I\left(M\in AA';I\in CC'\right)\) \(\left(1\right)\)
Lại có : \(AA'=CC'\left(cùng=BB'\right)\)
\(\Rightarrow AI=C'M\left(I\text{ là trung điểm }AA';M\text{ là trung điểm }CC'\right)\left(2\right)\)Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\text{ Tứ giác }AIC'M\text{ là hình bình hành }\)
\(\Rightarrow AI//C'M\left(2\text{ cạnh đối hình bình hành }\right)\\ \Rightarrow AI//mp\left(B'C'M\right)\)
Mà \(AD//B'C'\left(cùng//BC\right)\)
\(\Rightarrow AD//mp\left(B'C'M\right)\\ \Rightarrow mp\left(ADI\right)//mp\left(B'C'M\right)\) \(\)