Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

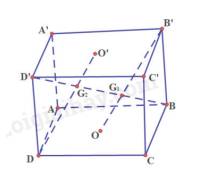
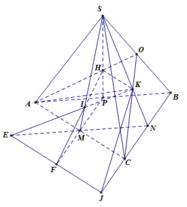
a) Ta có: AD // B’C’, AD = B’C’ nên ADC’B’ là hình bình hành
Suy ra AB’ // DC’ nên AB‘ // (A’C’D) (1)
Ta có: (ACC’A‘) là hình bình hành nên AC // A’C‘
Suy ra AC // (A’C’D‘) (2)
Mà AB‘, AC thuộc (ACB‘) (3)
Từ (1), (2), (3) suy ra (ACB‘) // (A‘C’D)
b) Gọi O, O’ lần lượt là tâm hình bình hành ABCD, A’B’C’D’
Trong (BDD’B’): B’O cắt BD’
Mà B’O thuộc (ACB’), BD’ cắt (ACB’) tại\({G_1}\)
Suy ra: B’O cắt BD’ tại\({G_1}\)
Tương tự, ta có: DO’ cắt BD’ tại\({G_2}\)
Ta có: tam giác \({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\) (do BD // B’D’)
Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)
Nên \(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{2}{3}\)
Do đó:\({G_1}\) là trọng tâm tam giác ACB’
Chứng minh tương tự ta có:\({G_2}\) là trọng tâm tam giác A’C’D
c) Ta có tam giác\({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\)
Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)
Nên \({G_1}B = \frac{1}{3}BD'(1)\)
Tương tự ta có:\(\frac{{{G_2}D'}}{{{G_2}B}} = \frac{{OD'}}{{DB}} = \frac{1}{2}\)
Nên \({G_2}D' = \frac{1}{3}{\rm{DD}}'(2)\)
Từ (1) và (2) suy ra\({G_1}B = {G_1}{G_2} = {G_2}D'\)

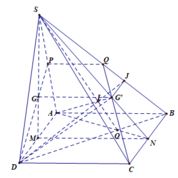
a: BD cắt AC tại E
b: Xét ΔSAC có SM/SA=SN/SC
nên MN//AC
c: Trong mp(SAC), ta có: SE không song song với MN
=>SE cắt MN tại K
d: \(C\in SN\)
\(C\in\left(ABCD\right)\)
Do đó: \(SN\cap\left(ABCD\right)=C\)

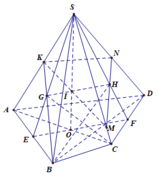
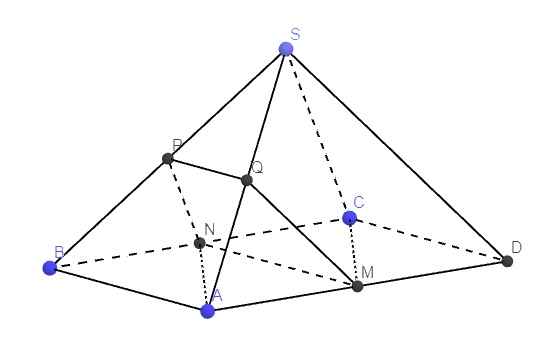
a. Do M, N là trung điểm AD, BC \(\Rightarrow MN||AB||CD\)
Gọi Q là trung điểm SA
\(\Rightarrow PQ\) là đường trung bình tam giác SAB
\(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow Q\in\left(MNP\right)\)
\(\Rightarrow Q=SA\cap\left(MNP\right)\)
b. Do Q là trung điểm SA, M là trung điểm AD
\(\Rightarrow MQ\) là đường trung bình tam giác SAD \(\Rightarrow MQ||SD\)
Mà \(MQ\in\left(MNP\right)\Rightarrow SD||\left(MNP\right)\)
Tương tự ta có \(NP||SC\) (đường trung bình) (1)
\(\left\{{}\begin{matrix}AM=NC=\dfrac{1}{2}AD\\AM||NC\end{matrix}\right.\) \(\Rightarrow AN||CM\) (2)
(1);(2) \(\Rightarrow\left(SMC\right)||\left(ANP\right)\)
c. Đề bài không tồn tại điểm L

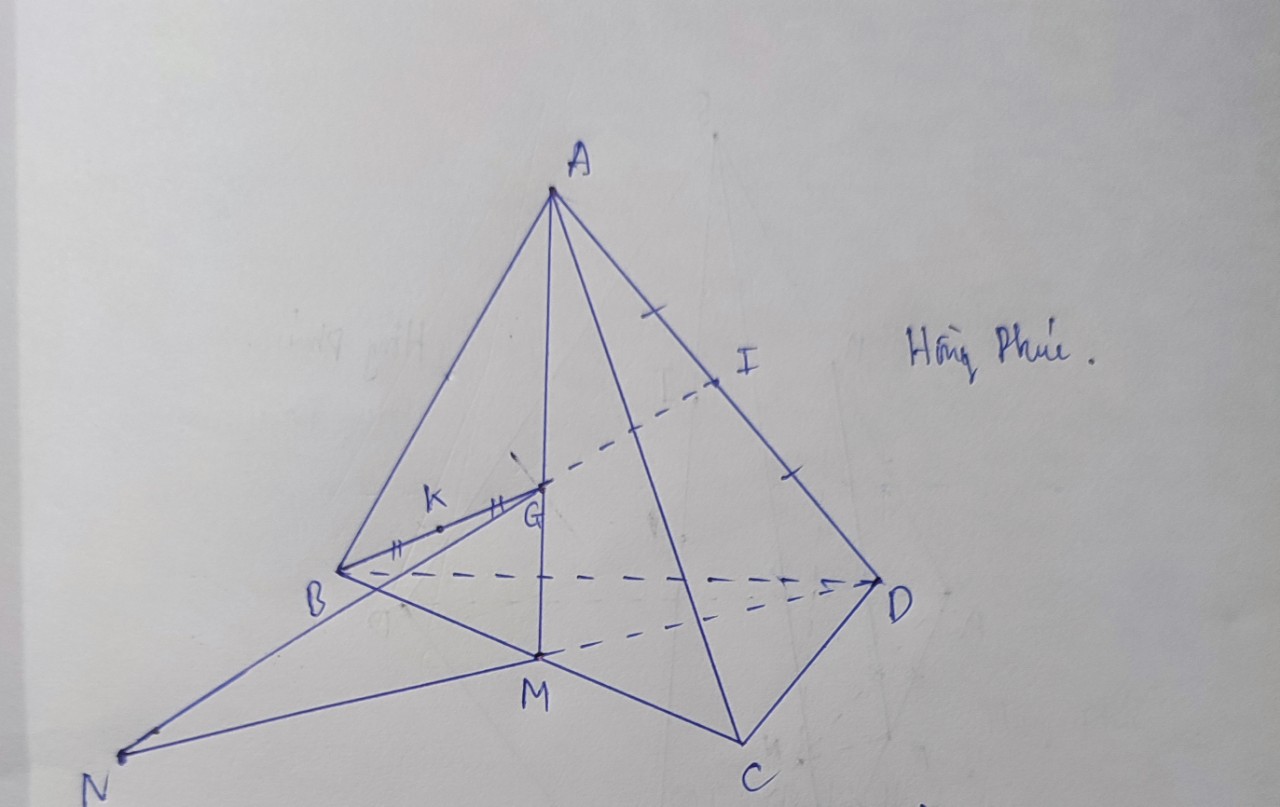
a) Xét (IJK) và (ACD)
có I thuộc (IJK) giao (ACD)
Trong (BCD) vẽ JK cắt CD tại E
=> E thuộc (IJK) giao (ACD) (đoạn này m ghi tắt :D)
Vậy IE là giao tuyến của (IJK) và (ACD)
Ta có E thuộc IE, IE là con của (IJK)
E thuộc CD
=> E là giao điểm của CD với (IJK)
b) Xét (ABD) và (IJK)
K thuộc (ABD) giao (IJK)
=> Kx là giao tuyến của (ABD) và (IJK)
mà AB // IJ
=> Kx // AB
Trong (ABD) vẽ Kx cắt AD tại F
=> F là giao điểm của AD và (IJK)
Ta có Kx // AB và Kx // IJ (cmt)
mà F thuộc Kx
=> KF // IJ