Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

⇒1/2AB=AM=1/2CD=CN
Mặt khác, M,N lần lượt là trung điểm của AB và CD
Do đó, AM//CN
Tứ giác AMCN có cặp cạnh đối vừa song song vừa bằng nhau nên là hình bình hành (đpcm)
b, Tứ giác AMCN là hình bình hành
⇒M1ˆ=N1ˆ (Hai góc đối của hình bình hành AMCN)
⇒M2ˆ=N2ˆ (Do M1ˆ và M2ˆ là hai góc kề bù; N1ˆ và N2ˆ là hai góc kề bù)
Mặt khác, ABCD là hình bình hành nên AB//CD ⇒B1ˆ=D1ˆ
ΔEDN và ΔKBM có:
M2ˆ=N2ˆ
DN=BM
B1ˆ=D1ˆ
⇒ΔEDN=ΔKBM(g.c.g)
⇒ED=KB (đpcm)
c, Gọi O là giao điểm của AC và BD.
ABCD là hình bình hành
⇒OA=OC
ΔCAB có:
MA=MB
OA=OC
MC cắt OB tại K
⇒ K là trọng tâm của ΔCAB
Mặt khác, I là trung điểm của BC
⇒ IA,OB,MC đồng quy tại K
Hoặc AK đi qua trung điểm I của BC

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
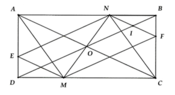
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.

Ta có ABCD là hình chứ nhật (gt)
=> AB = CD (t/c)
AB = BC(t/c)
góc ADM = góc NBC = 90 độ (t/c)
Xét tamgiác ADM và tam giác NBC có
NB = DM ( gt)
góc ADM = góc NBC = 90 độ ( cmt)
AD = BC ( cmt )
=> Tam giác ADM = Tam giác NBC ( c.g.c)
=> AM =NC ( 2 cạnh tương ứng )
Ta có AB = CD ( cmt )
DM = NB (gt)
mà AN+ NB = AB
DM + MC = DC
=> AN = MC
Xét tứ giác ANCM có
AM = NC ( cmt)
AN = MC (cmt)
=> tứ giác ANCM là Hình bình hành ( dhnb)
=> MN giao AC tại O
=> O là trung điểm của MN
=> M, O , N thẳng hàng
a: Xét tứ giác ANCM có
AN//CM
AN=CM
DO đó: ANCM là hình bình hành
b: Xét ΔBAC có NF//AC
nên NF/AC=BN/BA=DM/DC
Xét ΔDACcó EM//AC
nên EM/AC=DM/DC=NF/AC
=>EM=NF
Xét tứ giác NFME có
NF//ME
NF=ME
Do đó: NFME là hình bình hành
=>EN//FM và EN=FM