Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)Vì \(\Delta ABC\)vuông tại A (gt) => \(\widehat{BAC=90^0}hay\widehat{HÂ}K=90^0\)
Vì MH vông góc với AB tại H ( gt)
=>\(\widehat{MHA=90^0}\)
Vi MK vuông góc với AC tại K ( gt)
=> \(\widehat{MKA=90^0}\)
Xét tứ giác AMHK có :
\(\widehat{MKA=90^0\left(cmt\right)}\)
\(\widehat{MHA=}90^0\left(cmt\right)\)
\(\widehat{HAK=90^0\left(cmt\right)}\)
=> AMHK là hình chữ nhật ( dấu hiệu nhận biết)(đpcm)
2)a. Có : MH vuông góc với AB ( gt )
AC vuông góc với AB ( \(\Delta\)ABC vuông tại A)
=> MH//AC
Xét tam giác ABc có
MH//AC( cmt)
M là trung điểm BC (gt)
=> H là trung điểm AB (định lý đường trung bình của tam giác)(đpcm)
b. Có: MK vuông góc AC ( gt)
AB vuông góc AC( tam giác ABC vuông tại A )
=> MK//AB
Có:MK//AB(cmt)
M là trung điểm BC ( gt)
=> K là trung điểm AC ( định lý đường trung bình của tam giác )
Có : H là trung điểm AB ( cmt)
=. BH=\(\frac{1}{2}AB\)
Xét tam giác ABC có
M là trung điểm BC(cmt)
K là trung điểm AC ( cmt)
=> MK là đưởng trung bình của tam giác ABC( dấu hiệu nhận biết)
=> MK=\(\frac{1}{2}AB\)( tính chất đường trung bình của tam giác)
=> MK//AB(tính chất đường trung bình của tam giác) hay MK//BH
Có MK=\(\frac{1}{2}AB\)
BH= \(\frac{1}{2}AB\)
=> MK=BH
Mà MK//BH(cmt)
=> BMKH là hình bình hành
VÌ BMKH là hình bình hành (cmt)
=> Hai đường chéo HM và BK cắt nhau tại trung điểm mỗi đường
Mà E là trung điểm HM ( gt)
=> E là trung điểm BK hay ba điểm B; E; K thẳng hàng(dpcm)
3)a.Có MK//AB(cmt)
D thuộc MK
=> MD//AB
Có : BC//Ax( gt)
M thuộc BC; D thuộc Ax
=> BM//AD
Xét tứ giác ABMD có :
AB//MD(cmt)
BM//AD(cmt)
=> ABMD là hình bình hành (dấu hiệu nhận biết)
Xét tam giác ABC vuộng tại A có
M là trung điểm BC( gt)
=> AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}BC\)(tính chất )
Có M là trung điểm BC
=> BM=\(\frac{1}{2}BC\)
Mà AM=\(\frac{1}{2}BC\)
=> BM= AM
Vì ABMD là hình bình hành (cmt)
=> BM= AD(tính chất hình bình hành)
MÀ BM=AM
=> AD=AM(đpcm)
b.Xét tam giác AMD có
AM=AD(cmt)
=> Tam giác AMD cân tại A
Có AC vuông góc MK => AK vuông góc MD và AC vuông góc MD
Xét tam giác AMD cân tại A có :
AK vuông góc MD
=> AK là đường cao đồng thời là đường trung tuyến của tam giác AMD
Có AK là đường trung tuyến của tam giác AMD
=> K là trung điểm MD
Xét tứ giác AMCD có
K là trung điểm AC ( cmt0
K là trung điểm MD(cmt)
=> AMCD là hình bình hành (dấu hiệu nhận biết)
Mà đường chéo AC vuông góc với đương chéo MD
=> AMCD là hình thoi ( dấu hiệu nhận biết)
tưởng gì
a, xét tứ giác AHMK có
góc MHA=90 độ( MH ⊥ Ab-gt)
góc MKA=90 độ( MK⊥ AC-gt)
góc HAK= 90 độ ( tam giác ABC vuông tại A-gt)
-> AHMK là hcn ( tứ giác có 3 góc vuông là hcn) b)Có : MH vuông góc với AB ( gt )
AC vuông góc với AB (
Δ
ABC vuông tại A)
=> MH//AC
Xét tam giác ABc có
MH//AC( cmt)
M là trung điểm BC (gt)
=> H là trung điểm AB (định lý đường trung bình của tam giác)(đpcm)
. Có: MK vuông góc AC ( gt)
AB vuông góc AC( tam giác ABC vuông tại A )
=> MK//AB
Có:MK//AB(cmt)
M là trung điểm BC ( gt)
=> K là trung điểm AC ( định lý đường trung bình của tam giác )
Có : H là trung điểm AB ( cmt)
=. BH=1/2AB
Xét tam giác ABC có
M là trung điểm BC(cmt)
K là trung điểm AC ( cmt)
=> MK là đưởng trung bình của tam giác ABC( dấu hiệu nhận biết)
=> MK=1/2AB
( tính chất đường trung bình của tam giác)
=> MK//AB(tính chất đường trung bình của tam giác) hay MK//BH
Có MK=1/2AB
BH= 1/2AB
=> MK=BH
Mà MK//BH(cmt)
=> BMKH là hình bình hành
c)VÌ BMKH là hình bình hành (cmt)
=> Hai đường chéo HM và BK cắt nhau tại trung điểm mỗi đường
Mà E là trung điểm HM ( gt)
=> E là trung điểm BK hay ba điểm B; E; K thẳng hàng(dpcm)

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành

a) từ me vuông góc fc ab vuông góc fc=> me song song ab
=> mn song song ab => mn song song dc (1)
mà ab song song dc (do abcd là hbh)
từ ad ss bc (do .....)
=> md sscn (2) => ma ss bn (5)
từ (1)(2) => mndc là hbh (..) (3)
từ ab =2ad => ab=am=mdmà ab =dc (..) => md=dc (4)_
từ (3)(4) => mndc là hình thoi (...)
b) từ ne ss ab (cmt)
=> ne ss bf
mà nb = nc => fe=ec => e là tđ cf
c) từ abcd là hbh => a = dcb =60
từ mn ss ab và (5) => abnm là hbh (..)
ta có : mcd= 60\ 2 = 30
mà dcf + mcf +mcd
90=30 + mcf
mcf = 60 (6)
trong tam giác mfc có me là đcao đồng thời là đường tt
=> tam giác mfc cân tại M (7)
từ (6)(7) => mfc đều
d)từ fmc đều => fm=fc=> f thuộc trung trực mc
từ mn =nc => n thuộc trung trực mc
từ dm =dc => d thuộc trung trực mc
từ 3 ý trên => f,n,d thẳng hàng
(nếu đúng mình xin 1 tích nha :>> )
Giải thích các bước giải:
Ta có tứ giác ABCD là hbh
=> AD=BC; AD//BC
Mà M và N là trung điểm của AD và BC
=> MD=NC
Xét tứ giác MNCD có ;
MD//NC
MD=NC
=> Tứ giác MNCD là hbh
Mà MD=CD=AD/2
=> Tứ giác MNCD là hình thoi
b) Ta có tứ giác MNCD là hình thoi
=> CD//MN
Xét ΔBFC có: EN//BF
N là trung điểm của BC
=> EN là đườngtrung bình của tam giác BFC
=> E là trung điểm của CF
c) Ta có tứ giác MNCD là hình thoi
=> CM là tia phân giác của gốc BCD
=> Góc BCA=Góc BCD/2=60/2=30
Xét tam giác BFC có NE//BF
NE⊥FC
=> BF⊥FC
=> Góc BCF=90- góc FBC=90-góc BAD=30
=> Góc FCM=Góc FCB+ góc BCM=60
Xét tam giác MCF có ME vừa là đường cao vừa là trung tuyến
=> ΔMCF cân tại M
Mà góc MCF=60
=>ΔMCF đều
d) Ta có : FM=FC( do ΔMCF đều) => F∈ trung trực của MC
DM=DC(=AD/2) =>D∈trung trực của MC
Có NC=NM=> N∈trung trực của MC
=> F;N;D cùng thuộc trung trực của MC
=> F;N;D thẳng hàng

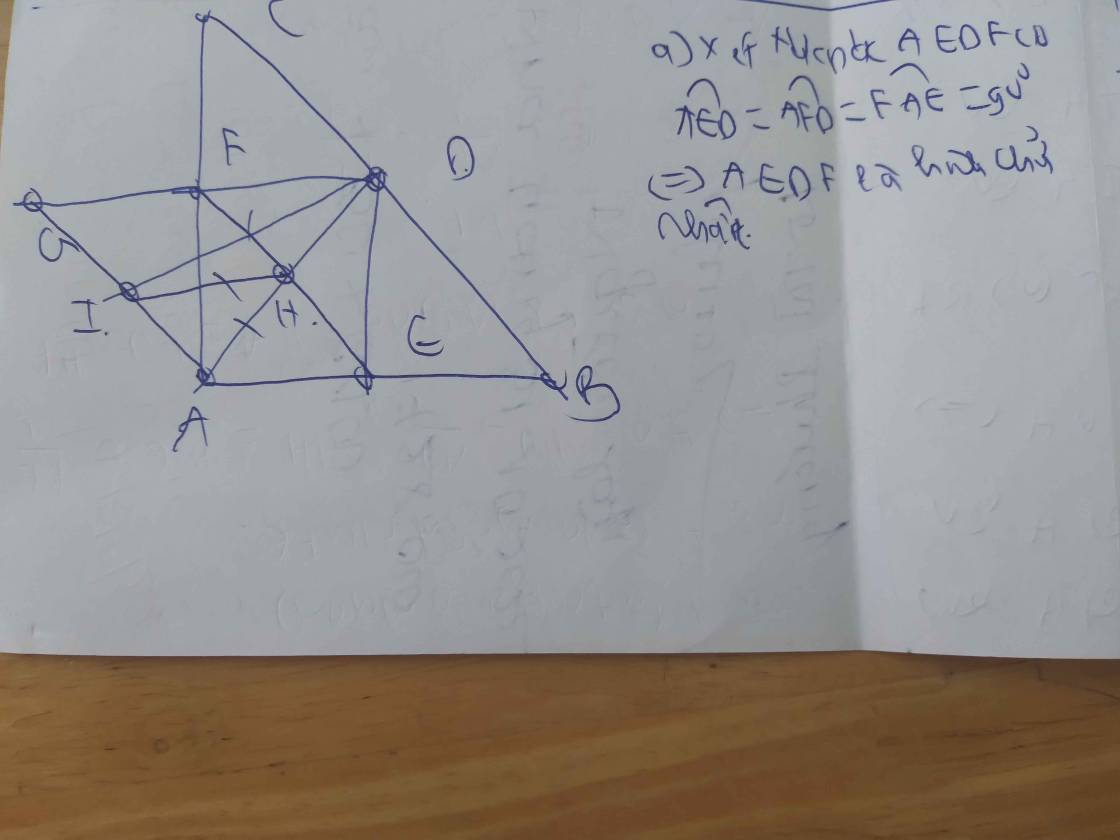



cứu với huhu
Xét ΔFDC có
H là trung điểm của FD
G là trung điểm của FC
Do đó: HG là đường trung bình
=>HG=1/2CD