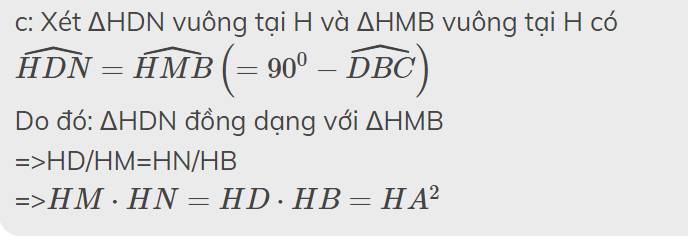Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ABCD là hình chữ nhật
=>AC=BD và AB^2+AD^2=BD^2
=>\(AB^2+AD^2=\left(4\sqrt{5}\right)^2=80\)
=>5AD^2=80
=>AD^2=16
=>AD=4
=>AB=8
ΔABD vuông tại A có AH là đường cao
nên AH*BD=AB*AD
=>AH*4căn 5=32
=>\(AH=\dfrac{8}{\sqrt{5}}\)
ΔABD vuông tại A có AH là đường cao
nên DH*DB=AD^2
=>\(DH\cdot4\sqrt{5}=4^2=16\)
=>\(DH=\dfrac{4}{\sqrt{5}}\)
Kẻ CK vuông góc BD, O là giao điểm của AC và BD
ABCD là hình chữ nhật
=>AC=BD và AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
=>DO=2căn 5
\(HO=2\sqrt{5}-\dfrac{4}{\sqrt{5}}=2\sqrt{5}-\dfrac{4\sqrt{5}}{5}=\dfrac{6\sqrt{5}}{5}\)
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
Do đó: ΔAHD=ΔCKB
=>AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
=>O là trung điểm của HK
=>HK=2*HO=12*căn 5/5
\(AK=\sqrt{AH^2+HK^2}=\dfrac{4\sqrt{65}}{5}\)
=>\(CH=\dfrac{4\sqrt{65}}{5}\)

a: \(\left\{{}\begin{matrix}AB^2+AD^2=BD^2=25\\\dfrac{1}{AB^2}+\dfrac{1}{AD^2}=\dfrac{1}{AH^2}=\dfrac{25}{144}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=4\left(cm\right)\\AC=3\left(cm\right)\end{matrix}\right.\)
\(\Leftrightarrow S_{ABCD}=AB\cdot AC=12\left(cm^2\right)\)