Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

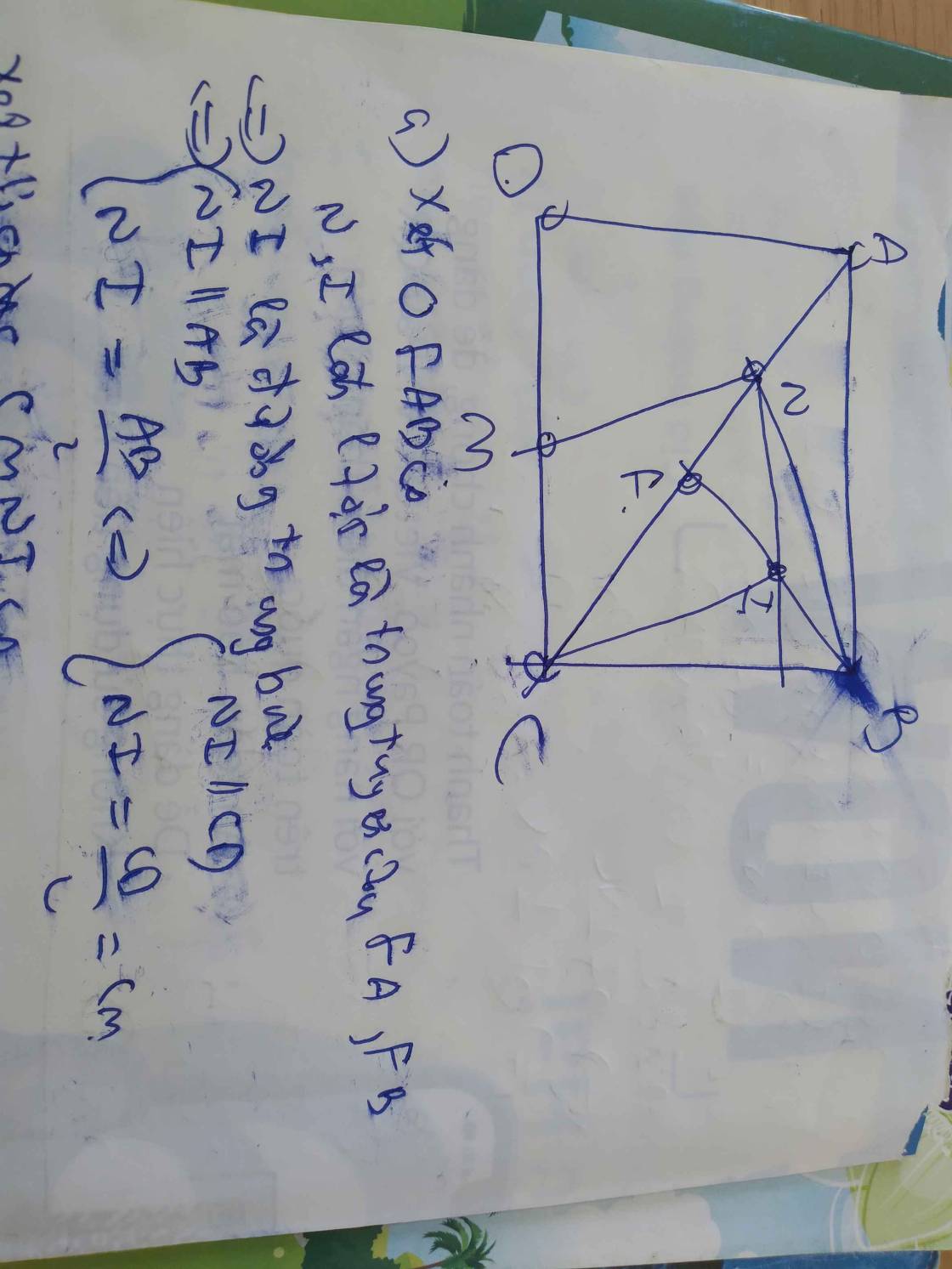
a)Vì A đối xứng với F qua N =>N là trung điểm AF
Mà I là trung điểm BF(gt) => NI là đường trung bình của tam giác FAB
=>NI//AB,NI=1/2AB .Mà AB//CD(ABCD là hình chữ nhật) =>NI//CD hay NI//MC(M thuộc CD) (1)
Vì NI=1/2AB(cmt), AB=CD(ABCD là hcn) => NI=1/2CD
Lại có: M là trung điểm CD(gt) => MC=MD=1/2CD =>NI=MC (2)
Từ (1) và (2) => CINM là hình bình hành
b)Vì NI//CD (cmt), CD vuông góc với BC(ABCD là hình bình hành)
=>NI vuông góc với BC =>NI là đường cao trong tam giác NBC (3)
Vì góc BNM=90 độ(gt) =>BN vuông góc với NM
Lại có :NM//IC(CINM là hình bình hành) =>CI vuông góc với BN
=>CI là đường cao trong tam giác BNC (4)
Từ (3) và (4) =>I là trực tâm trong tam giác BNC =>BI vuông góc với AC hay BF vuông góc với AC

Có DAB + ABC = 180
Có DAC + CAB = 90 và CBF + FBA = 90
Từ 2 điều trên suy ra FBA + FAB = 90
Xét tam giác ABF có FBA + FAB = 90 (cm trên)
và FBA + FAB + AFB = 180 (3 góc tam giác)
Từ đó suy ra được AFB = 90.
Từ đó biết được đpcm

a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật

a, Vì \(\widehat{AEM}=\widehat{AFM}=\widehat{EAF}=90^0\) nên AEMF là hcn
b, Vì M là trung điểm BC, MF//AB(⊥AC) nên F là trung điểm AC
Mà F là trung điểm MN nên AMCN là hbh
c, Để AMCN là hcn thì \(\widehat{AMC}=90^0\) hay AM là đường cao tam giác ABC
Mà AM là trung tuyến nên để AMCN là hcn thì ABC vuông cân tại A