Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//DC)
Do đó: ΔAHB\(\sim\)ΔBCD(g-g)
b) Xét ΔBCD có CE là đường phân giác ứng với cạnh BD(gt)
nên \(\dfrac{EB}{ED}=\dfrac{BC}{CD}\)(Tính chất đường phân giác của tam giác)(1)
Ta có: ΔAHB\(\sim\)ΔBCD(cmt)
nên \(\dfrac{AH}{BC}=\dfrac{HB}{CD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AH}{HB}=\dfrac{BC}{CD}\)(2)
Từ (1) và (2) suy ra \(\dfrac{AH}{HB}=\dfrac{EB}{ED}\)
hay \(AH\cdot ED=HB\cdot EB\)(đpcm)

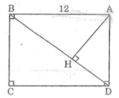
a) Xét tam giác AHB và tam giác BCD ta có:
AHB = BCD (=90^0)
ABH = BDC (AB // CD và 2 góc slt)
=> Tam giác AHB đồng dạng với tam giác BCD (G-G)
b) Tam giác BCD vuonng tại C. Áp dụng Pitago ta tính được BD = 15cm
Tam giác AHB đồng dạng với tam giác BCD (G-G)
\(\Rightarrow\dfrac{AH}{BC}=\dfrac{AB}{BD}\Rightarrow\dfrac{AH}{9}=\dfrac{12}{15}\)
=> AH = 7,2 cm
c) Tam giác AHB vuông tại H. Áp dụng Pitago ta tính được HB = 9,6cm
\(S_{AHB}=\dfrac{1}{2}AH.HB=\dfrac{1}{2}.7,2.9,6=34,56\left(cm^2\right)\)

a)
vì ABCD hình chữ nhật nên ta có AB//CD
=> góc ABH= góc BDC ( so le trong, AB//CD)
xét tam giác AHB,BCD có
góc A= góc C =90
góc ABH=BDC(cmt)
=> tam giác AHB đồng dạng với tam giác CDB (gg)
b)
vì ABCD hcn nên
AB=CD=12
BC=AD=9
AD Đlí pytado cho tam giác vuông CDB có
BD2=BC2+DC2
BD2=81+144
BD=15cm
theo câu a) ta có
AH/AB=BC/BD
=> AH= AB.BC chia BD
AH= 12.9 chia 15
AH= 7.2CM
C)
BD

a) Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
góc ABH = góc BDC(hai góc so le trong, AB//DC)
góc BCD = góc AHB(hai góc vuông)
Do đó: ΔAHB∼ΔBCD(g-g)
b) Xét ΔBCD có CE là đường phân giác ứng với cạnh BD(gt)
nên \(\dfrac{EB}{ED}\)=\(\dfrac{BC}{CD}\)(Tính chất đường phân giác của tam giác)(1)
Ta có: ΔAHB∼∼ΔBCD(cmt)
nên\(\dfrac{AH}{BC}\)=\(\dfrac{HB}{CD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay\(\dfrac{AH}{BH}\)=\(\dfrac{BC}{CD}\)(2)
Từ (1) và (2) suy ra \(\dfrac{AH}{BH}\)=\(\dfrac{EB}{ED}\)
hay AH⋅ED=HB⋅EB(đpcm)

a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)
Do đó: ΔAHB~ΔBCD
b: ta có: ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD^2=12^2+5^2=169\)
=>\(BD=\sqrt{169}=13\left(cm\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot13=12\cdot5=60\)
=>\(AH=\dfrac{60}{13}\left(cm\right)\)
c: Xét ΔBCD có CE là phân giác
nên \(\dfrac{EB}{ED}=\dfrac{BC}{CD}\)(1)
Xét ΔHAB vuông tại H và ΔADB vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHAB~ΔADB
=>\(\dfrac{HA}{AD}=\dfrac{HB}{AB}\)
=>\(\dfrac{HA}{HB}=\dfrac{AD}{AB}=\dfrac{BC}{CD}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{EB}{ED}=\dfrac{HA}{HB}\)
=>\(EB\cdot HB=HA\cdot ED\)

a, Vì ABCD là hình chữ nhật nên AB// DC => góc ABD = BDC ( hai góc đối đỉnh)
Xét tam giác AHB và tam giác BCD có
góc AHB = góc BCD =90 ĐỘ
góc ABD = BDC ( cmtrên)
Suy ra .............( g.g)
Vì ABCD là hcn nên AB =DC =20
BC=AD=15
Theo định lí Pitago trong tam giác BCD
\(BD^2=BC^2+DC^2\)
\(BD^2=20^2+15^2\)
\(BD^2=625\)
BD = 25
Theo a ta có \(\frac{AH}{AB}=\frac{BC}{BD}\)
NÊN \(AH=\frac{AB\cdot BC}{BD}\)
\(AH=\frac{20\cdot15}{25}\)
AH=12
c, d tự trả lời
e hình như dựa một chút vào tình chất đường phân giác trong tam giác

1: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó:ΔAHB\(\sim\)ΔBCD
2: Ta có: ΔAHB\(\sim\)ΔBCD
nên \(\dfrac{BC}{AH}=\dfrac{CD}{HB}\)
hay BC/CD=AH/HB
mà BC/CD=EB/ED
nên EB/ED=AH/HB
hay \(EB\cdot HB=AH\cdot ED\)

Vì
△
AHB đồng dạng
△
BCD với tỉ số đồng dạng: 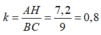
Ta có:  =
k
2
=
0
,
8
2
= 0,64 ⇒
S
A
H
B
=
0
,
64
.
S
B
C
D
=
k
2
=
0
,
8
2
= 0,64 ⇒
S
A
H
B
=
0
,
64
.
S
B
C
D
S B C D = 1/2 BC.CD = 1/2 .12.9 = 54( c m 2 )
Vậy S A H B = 0 , 64 . S B C D = 0,64.54 = 34,56 ( c m 2 ).