Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

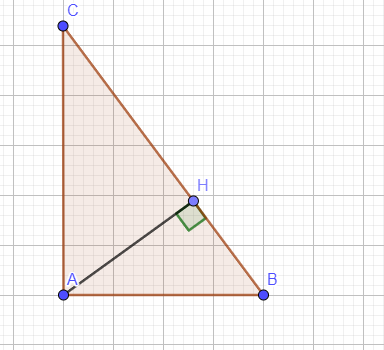
Áp dụng định lý pytago ta có :
`AC^2+AB^2=BC^2`
hay `16^2+12^2=BC^2`
`=>BC^2=400`
`=>BC=20(cm)`

a) Xét tứ giác EHFA có :
BAC = 90*
HF \(\perp\)AC(gt)
HE\(\perp\)AB (gt)
=> EHFA là hình chữ nhật
=> AH = EF
b) Vì EHFA là hình chữ nhật (cmt)
=> EH//AF , EH= AF
Mà E là trung điểm PH
=> PE = EH
=> PE = AF
Xét tứ giác PEFA có :
PE = AF
PE// AF ( EH//AF , E\(\in\)PH )
=> PEFA là hình bình hành
d) Vì PEFA là hình bình hành (cmt)
=> FE//PA (1)
Ta có : HF = FQ (gt)
MÀ HF = EA
=> FQ = EA
Xét \(\Delta HAQ\)có :
AF là trung trực
=> \(\Delta HAQ\) cân tại A
=> AH = AQ
Mà AH = EF (cmt)
=> EF = AQ
Xét tứ giác EFQA ta có :
EF = AQ
EA = FQ
=> EFQA là hình bình hành
=> EF// AQ(2)
(1)(2) => P,A,Q thẳng hàng

a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật
b: Xét ΔAEB có
H là trung điểm của EB
M là trung điểm của AB
Do đó: HM là đường trung bình
=>HM//AE và HM=AE/2
hay HD//AE và HD=AE
hay ADHE là hình bình hành

a: Xét ΔAND và ΔABM có
góc A chung
AN=DM
AB=AD
=>ΔAND=ΔABM
=>AN=AM
góc NAD=góc BAM
=>góc NAD+góc DAM=góc DAM+góc BAM=90 độ
=>góc NAM=90 độ
=>ΔNAM vuông cân tại A
b: Xét ΔABM và ΔPDA có
góc B=góc D
góc BAM=góc APD
=>ΔABM đồng dạng với ΔPDA
=>AB/BM=PD/AD
=>AB*AD=BM*PD=BC^2
c: Xét ΔAIH và ΔAQD có
góc A chung
góc H=góc D
=>ΔAIH đồng dạng với ΔAQD
=>AI*AD=AH*AQ
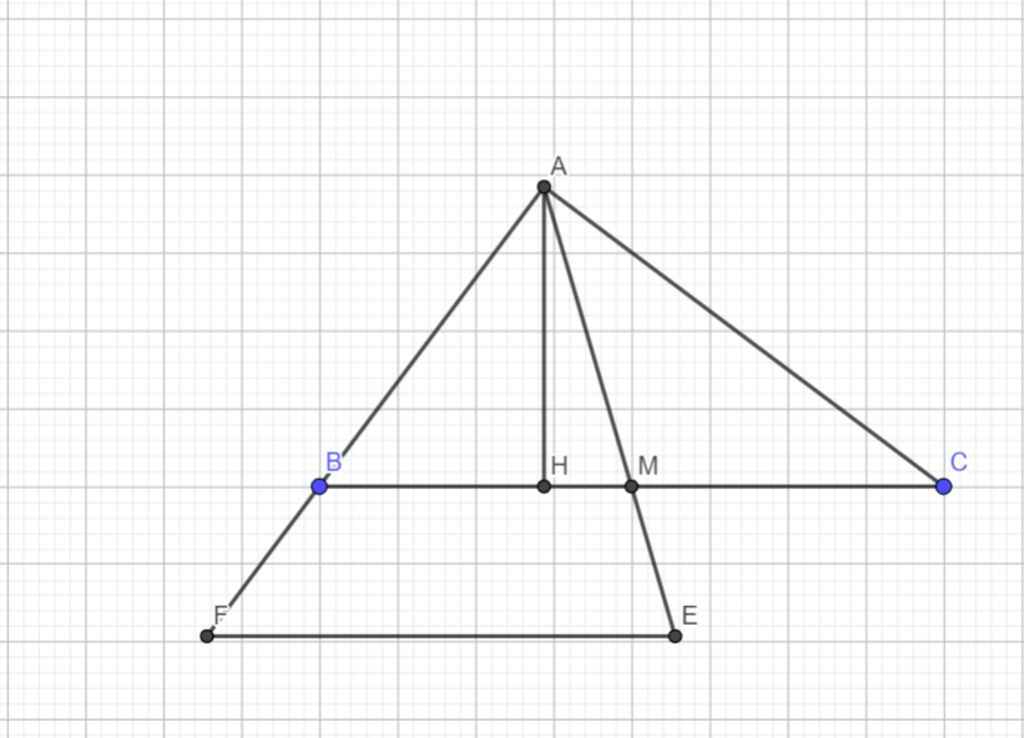
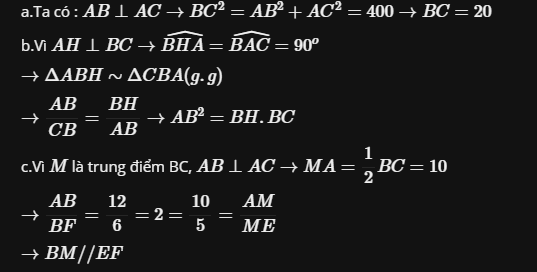
\(BD=\sqrt{16^2+12^2}=20\left(cm\right)\)
AH=12*16/20=192/20=9,6cm
MH=9,6-4=5,6cm
DH=12^2/20=144/20=7,2cm
=>HN=7,2-3=4,2cm
=>HN/HD=HM/HA
=>MN//AD
=>MN vuông góc AB
Xét ΔANB có
AH,NM là đường cao
AH cắt NM tại M
=>M là trực tâm
=>BM vuông góc AN