Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo nhé !
a) Nửa chu vi hay tổng chiều dài và chiều rộng của hình chữ nhật là:
60 : 2 = 30 (cm)
Chiều dài AB gấp rưỡi chiều rộng BC nghĩa là chiều dài bằng \(\frac{3}{2}\) chiều rộng
Chiều dài: |---|---|---|
Chiều rộng: |---|---|
Tổng số phần bằng nhau là:
3 + 2 = 5 (phần)
Chiều dài AB của hình chữ nhật có độ dài là:
30 : 5 × 3= 18 (cm)
Chiều rộng BC của hình chữ nhật là:
30−18 = 12 (cm)
Diện tích của hình chữ nhật ABCD là:
12 . 18 = 216 (cm2)
b) Ta có SEAB=SBCD
Vì:
- ΔEAB có chiều cao hạ từ E lên đáy AB bằng chiều cao BC của tam giác BCD hạ từ B lên đáy DC,
- đáy AB=DC
SABM=SDBM
Vì:
- chiều cao AB=DC
- chung đáy BM
Nên ta có: SEAB−SABM=SBCD−SDBM
Hay SMBE=SMCD
c) SABM =\(\frac{2}{3}\).SMAD
Vì:
- Đường cao AB bằng đường cao hạ từ đỉnh M của ΔMAD
- Đáy BM = \(\frac{2}{3}\)BC = \(\frac{2}{3}\)AD
Mà 2 tam giác này chung đáy AM nên suy ra chiều cao hạ từ đỉnh B lên AM của ΔMAB bằng \(\frac{2}{3}\) chiều cao hạ từ đỉnh D của ΔMAD lên đáy AM.
Đây cũng là chiều cao từ các đỉnh hạ lên đáy MO
ΔMBO và ΔMDO chung đáy MO
Chiều cao hạ từ B lên đáy MO của ΔMBO bằng \(\frac{2}{3}\)chiều cao hạ từ đỉnh DD lên đáy MO của ΔMDO
⇒\(\frac{SMBO}{SMOD}\) = \(\frac{2}{3}\)
ΔMBO và ΔMDO chung chiều cao hạ từ M lên BD
⇒\(\frac{OB}{OD}=\frac{2}{3}\)
k nha
đúng![]()
a) Nửa chu vi hay tổng chiều dài và chiều rộng của hình chữ nhật là:
60:2=3060:2=30 (cm)
Chiều dài AB gấp rưỡi chiều rộng BC nghĩa là chiều dài bằng 3232 chiều rộng
Chiều dài: |---|---|---|
Chiều rộng: |---|---|
Tổng số phần bằng nhau là:
3+2=53+2=5 (phần)
Chiều dài AB của hình chữ nhật có độ dài là:
30:5×3=1830:5×3=18 (cm)
Chiều rộng BC của hình chữ nhật là:
30−18=1230−18=12 (cm)
Diện tích của hình chữ nhật ABCD là:
12.18=21612.18=216 (cm2)(cm2)
b) Ta có SEAB=SBCDSEAB=SBCD
Vì:
- ΔEABΔEAB có chiều cao hạ từ E lên đáy AB bằng chiều cao BC của tam giác BCD hạ từ B lên đáy DC,
- đáy AB=DC
SABM=SDBMSABM=SDBM
Vì:
- chiều cao AB=DC
- chung đáy BM
Nên ta có: SEAB−SABM=SBCD−SDBMSEAB−SABM=SBCD−SDBM
Hay SMBE=SMCDSMBE=SMCD
c) SABM=23.SMADSABM=23.SMAD
Vì:
- Đường cao AB bằng đường cao hạ từ đỉnh M của ΔMADΔMAD
- Đáy BM=23.BC23.BC=2323AD
Mà 2 tam giác này chung đáy AM nên suy ra chiều cao hạ từ đỉnh B lên AM của ΔMABΔMAB bằng 2323 chiều cao hạ từ đỉnh D của ΔMADΔMAD lên đáy AM.
Đây cũng là chiều cao từ các đỉnh hạ lên đáy MO
ΔMBOΔMBO và ΔMDOΔMDO chung đáy MO
Chiều cao hạ từ B lên đáy MO của ΔMBOΔMBO bằng 2323 chiều cao hạ từ đỉnh DD lên đáy MO của ΔMDOΔMDO.
⇒SMBOSMDO=23⇒SMBOSMDO=23
ΔMBOΔMBO và ΔMDOΔMDO chung chiều cao hạ từ M lên BD
⇒OBOD=23⇒OBOD=23.


Trả lời :
Bạn vào đây tham khảo nha , dài quá mk nhác viết :
https://olm.vn/hoi-dap/detail/10534222471.html
~ Study well ~
#)Giải :
a) Chiều dài hình chữ nhật ABCD là :
60 : 2 : ( 3 + 2 ) x 3 = 18 ( cm )
Chiều rộng hình chữ nhật ABCD là :
60 : 2 : ( 3 + 2 ) x 3 = 12 ( cm )
Diện tích hình chữ nhật ABCD là :
18 x 12 = 216 ( cm2)
b) Diện tích hình tam giác ABE là :
18 x 12 : 2 = 108 ( cm2)
Diện tích hình tam giác ABM là :
18 x ( 12 : 3 x 2 ) : 2 = 72 ( cm2)
Diện tích hình tam giác MBE là :
108 - 72 = 36 ( cm2)
Diện tích hình tam giác MCD là :
18 x ( 12 - 8 ) : 2 = 36 ( cm2)
Vậy diện tích tam giác MBE = diện tích tam giác MCD

bn vào tìm bn tên nguyenngocyennhi đi ở đó có bài toán bn cần đó
help me mk có ít điểm quá kb mk luôn nha

1)
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)
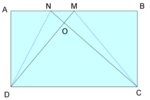
Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
2)

Ta có:
MN = 1/2 AB - 1/3 AB = 1/6 AB
Xét tam giác NMD và MCD có chiều cao = chiều rộng hình chữ nhật mà đáy NM = 1/6 CD => S_NMD = 1/6 S_MCD. Mà S_MCD = 360 : 2 = 180 (cm2) => S_NMD = 180 : 6 = 30 (cm2)
Mặt khác 2 tam giác này chugn đáy MD => Chiều cao tam giác NMD đỉnh N = 1/6 chiều cao tam giác MCD đỉnh C
Xét tam giác NMD và NMC chung đáy NM chiều cao bằng nhau => S_NMD = S_NMC = 30 (cm2)
Xét tam giác NMO và MCO có chung đáy MO chiều cao tam giác NMO = 1/6 chiều cao MCO => S_NMO = 1/6 S_MCO
Vậy diện tích NMO là : 30 : (1 + 6) = 30/7 (cm2
3)
AB=a ; BC=b
Diện tích hình chữ nhật: S=a.b
S_ADN= 2/3a x b : 2 = 1/3 ab = 1/3S
Ta có:
S_AMN = (S_AMC + S_ANC) – S_MCN= (MC x AB :2 + NC x AD : 2) – (NC x MC : 2)
= (1/2b x a : 2 + 1/3a x b : 2) – (1/3a x 1/2b : 2)
= ¼ S + 1/6S - 1/12S
= 5/12 S – 1/12 S = 4/12 S = 1/3 S
Gọi S=a x b
S_tăng = 3/2a x 3/2b = 9/4 S
Diện tích mới: 360 x 9/4 = 810 (cm2)
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
