Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

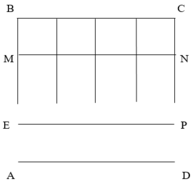
Trước hết Ta xét các hình chữ nhật tạo bởi hai đoạn AD, EP và các đoạn nối các điểm trên hai cạnh AD và BC. Bằng cách tương tự như tronh ví dụ 1 ta tính được 10 hình.
Tương tự ta tính được số hình chữ nhật tạo thành do hai đoạn EP và MN, do MN và BC đều bằng 10.
Tiếp theo ta tính số hình chữ nhật tạo thành do hai đoạn AD và MN, EP và BC với các đoạn nối các điểm trên hai cạnh AD và BC đều bằng 10.
Vì vậy :
Số hình chữ nhật đếm được trên hình vẽ là :
10 + 10 + 10 + 10 + 10 + 10 = 60 (hình)
Đáp số 60 hình.

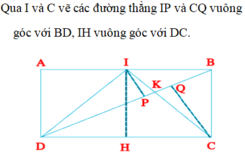
Qua I và C vẽ các đường thẳng IP và CQ vuông góc với BD, IH vuông góc với DC.
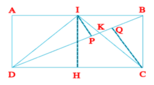



Qua I và C vẽ các đường thẳng IP và CQ vuông góc với BD, IH vuông góc với DC.
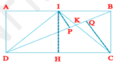
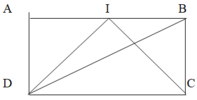
Ta có S A D B = S C D B = 1 2 S A B C D và S D I B = 1 2 S A D B (vì có chung đường cao DA, IB = 1/2 AB),
S D I B = 1 2 S D B C . Mà 2 tam giác này có chung đáy DB
Nên IP = 1/2 CQ. S I D K = 1 2 S C D K (vì có chung đáy DK và IP = 1/2 CQ)
S C D I = S I D K + S D K C = 3 S D I K .
Ta có :
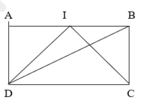
S A D I = 1 2 AD x AI, S D I C = 1 2 IH x DC
Mà IH = AD, AI = 1/2 DC, S D I C = 2 S A D I n ê n S A D I = 3 2 S D I K
Vì AIKD là phần được tô màu vàng nên S A I K D = 20 ( c m 2 )
S D A I + S I D K = 20 ( c m 2 )
S D A I + 2 3 S A D I = 20 ( c m 2 )
S D A I = (3 x 20)/5 = 12 ( c m 2 ) ;
Mặt khác S D A I = 1 2 S D A B = 1 4 S A B C D