Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.

Bài 2:
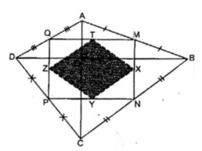
Xét ΔMQN có
A là trung điểm của MN
D là trung điểm của MQ
Do đó: AD là đường trung bình
=>AD//NQ và AD=NQ/2(1)
Xét ΔNPQ có
B là trung điểm của NP
C là trung điểm của QP
Do đó: BC là đường trung bình
=>BC//NQ và BC=NQ/2(2)
Từ (1) và (2) suy ra AD//BC và AD=BC
hay ABCD là hình bình hành

Giải thích các bước giải:
a/ Trong ΔABCΔABC có N,PN,P lần lượt là trung điểm của BC,ACBC,AC
⇒ NPNP là đường trung bình ΔABCΔABC
⇒ NP//AB//CDNP//AB//CD (1)
Trong ΔBCDΔBCD có N,QN,Q lần lượt là trung điểm của BC,BDBC,BD
⇒ NQNQ là đường trung bình ΔBCDΔBCD
⇒ NQ//CD//ABNQ//CD//AB (1)
Trong hình thang ABCDABCD có M,NM,N lần lượt là trung điểm của AD,BCAD,BC
⇒ MNMN là đường trung bình hình thang ABCDABCD
⇒ MN//AB//CDMN//AB//CD (3)
Từ (1) (2) và (3) suy ra: M,N,P,QM,N,P,Q thằng hàng
Hay M,N,P,QM,N,P,Q nằm trên một đường thẳng
b/ Vì MNMN là đường trung bình thang ABCDABCD
nên MN=AB+CD2=a+b2MN=AB+CD2=a+b2
Ta có: NPNP là đường trung bình ΔABCΔABC
⇒ NP=AB2=a2NP=AB2=a2
Ta lại có: NQNQ là đường trung bình ΔBCDΔBCD
⇒ NQ=CD2=b2NQ=CD2=b2
Vì a>b nên PQ=NP−NQ=a2−b2=a−b2PQ=NP−NQ=a2−b2=a−b2
c/ Ta có: MN=MP+PQ+QNMN=MP+PQ+QN
⇒a+b2=3.a−b2⇒a+b2=3.a−b2
⇒a+b=3a−3b⇒a+b=3a−3b
⇒3a−a=b+3b⇒3a−a=b+3b
⇒2a=4b⇒2a=4b
⇒a=2b⇒a=2b
Chúc bạn học tốt !!!
^HT^

Bài này ko khó lắm đâu. Bạn chỉ cần nghĩ một chút thôi.
a,Nối A với C.
Xét tam giác BAC có: M là trung điểm của AB, N là trung điểm của BC
Suy ra: MN là đường trung bình của tam giác BAC
Nên MN song song với BC.(1)
Xét tam giác ACD có: P là trung điểm của CD và Q là trung điểm của AD.
Do đó: PQ là đường trung bình của tam giác ACD
Nên PQ song song với BC. (2)
Từ (1) và (2), ta có: MN song song với PQ.
b, Xét tam giác MQP có: I là trung điểm của MQ, K là trung điểm của MP
Vì thế IK là đường trung bình của tam giác MQP
Suy ra: IK song song với PQ.
Tương tự, KH là đường trung bình của tam giác MNP
Nên KH song song với MN.
Mà MN song song với PQ
Do đó: KH song song với PQ
Qua điểm K nằm ngoài đường thẳng PQ, có 2 đường thẳng IK,KH cùng song song với PQ nên theo tiên đề Ơclít , 3 điểm I,K,H thẳng hàng.
Chúc bạn học tốt.

Xét ΔMNQ có
A là trung điểm của MN
D là trung điểm của MQ
Do đó: AD là đường trung bình của ΔMNQ
Suy ra: AD//NQ và AD=NQ/2(1)
Xét ΔNPQ có
B là trung điểm của NP
C là trung điểm của QP
Do đó: BC là đường trung bình của ΔNPQ
Suy ra: BC//NQ và BC=NQ/2(2)
Từ (1) và (2) suy ra AD//BC và AD=BC
Xét ΔMNP có
A là trung điểm của MN
B là trung điểm của NP
Do đó: AB là đường trung bình của ΔMNP
Suy ra: AB=MP/2=NQ/2(3)
Từ (1) và (3) suy ra AD=AB
Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
mà AB=AD
nên ABCD là hình thoi
