Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quay quanh AB thì ta có r = BC = a , h = AB = 2a.
⇒ V1 = πr2h = π.a2.2a = 2πa3
Quay quanh BC ta có r = AB = 2a, h = BC = a
⇒ V2 = πr2h = π.(2a)2.a = 4πa3
⇒ V2 = 2V1
Vậy chọn C.

Quay quanh AB thì ta có r = BC = a , h = AB = 2a.
⇒ V 1 = π r 2 h = π ⋅ a 2 ⋅ 2 a = 2 π a 3
Quay quanh BC ta có r = AB = 2a, h = BC = a
⇒ V 2 = π r 2 h = π ⋅ ( 2 a ) 2 ⋅ a = 4 π a 3 ⇒ V 2 = 2 V 1
Vậy chọn C.

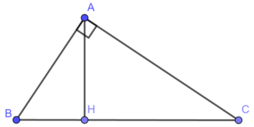
Đặt AB = c, AC = b, BC = a, AH = h là đường cao kẻ từ đỉnh A đến cạnh huyền BC
Vì tam giác ABC vuông tại A nên ta có: h = bc/a
*Khi quay tam giác vuông ABC một vòng quanh cạnh huyền BC thì cạnh AB và AC vạch nên hai hình nón chung đáy có bán kính đáy bằng đường cao AH và tổng chiều cao hai hình nón bằng cạnh huyền BC
Thể tích của hai hình nón:
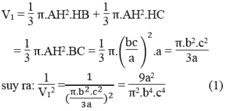
Khi quay tam giác vuông ABC một vòng quanh cạnh AB thì ta thu được hình nón có chiều cao AB = c, bán kính đáy AC = b
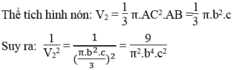
Khi quay tam giác vuông ABC một vòng quanh cạnh AC thì ta thu được hình nón có chiều cao AC=b,bán kính đáy AB=c
Thể tích hình nón:
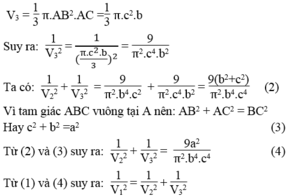

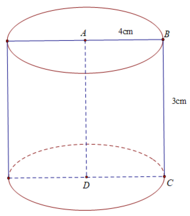
b) Thể tích hình trụ bằng :
V = π R 2 h = π 4 2 .3 = 48π( c m 3 )

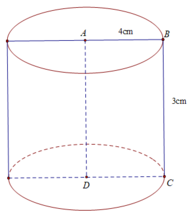
a) Diện tích xung quanh của hình trụ bằng:
S x q = 2πRh = 2π.4.3 = 24π ( c m 2 )

Khi quay hình chữ nhật ABCD quanh đường AB thì được hình trụ có
R=BC=a, h=AB=2a
\(S_{XQ}=2\cdot pi\cdot a\cdot2a=4\cdot pi\cdot a^2\)

Hướng dẫn trả lời:
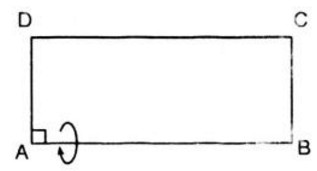
Theo đề bài ta có:
Diện tích hình chữ nhật ABCD là: AB.AD = 2a2 (1)
Chu vi hình chữ nhật là: 2(AB + CD) = 6a ⇒ AB + CD = 3a (2)
Từ (1) và (2), ta có AB và CD là nghiệm của phương trình:
x2 – 3ax – 2a2 = 0
Giải phương trình ta được x1 = 2a; x2 = a
Theo giả thiết AB > AD nên ta chọn AB = 2a; AD = a
Vậy diện tích xung quanh hình trụ là:
Sxq = 2π . AD . AB = 2π . a . 2a = 4 πa2
Thể tích hình trụ là:
V = π . AD2 . AB = π. a2 . 2a = 2πa3
Giải:
Quay quanh AB thì ta có r = a, h= 2a.
nên V1 = πr2h = π.a2.2a = 2πa3
Quay quanh BC thì ta có r = 2a, h = a
nên V2 = πr2h = π(2a)2.a = 4πa3
Do đó 2V1 = V2
Vậy chọn C