Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

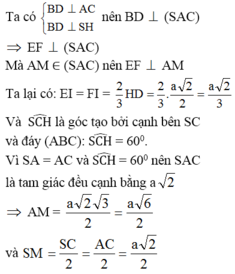

Điều này chứng tỏ SM là đường cao của hình chóp S.AEMF. Vậy thể tích của khối chóp S.AEMF là:
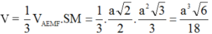

Đáp án B
Hướng dẫn giải:
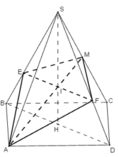
Gọi H là tâm của đáy khi đó S H ⊥ ( A B C D )
Lại có S H = H A tan 60 o = a 6 2
V S . A B C D = 1 3 S H . S A B C D = a 3 6 6
Mặt khác, gọi G = S H ∩ A M
⇒ G là trọng tâm của tam giác SAC.
Do đó S G S H = 2 3
Qua G dựng đường thẳng song song với BD cắt SB, SD lần lượt tại P và Q
Khi đó V S . A B M V S . A B C = S P S B . S M S C = 1 3
từ đó suy ra V S . A P M Q V S . A B C D = 1 3
Do vậy V S . A P M Q = a 3 6 18
⇒ 18 V a 3 = 6

Đáp án B
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.
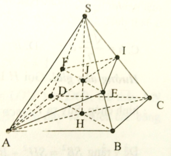
Dễ thấy I là trung điểm của SC, vì BD ⊥ SC, nên BD//(P). Do đó EF // BD. Để ý rằng EF đi qua trọng tâm J của tam giác SDB.
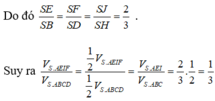

Để tính thể tích SAPMQ, ta cần tìm độ dài đoạn PM và đoạn MQ. Gọi E là trung điểm của BD. Ta có ME song song với AM và ME = 1/2 BD = 1/2 a. Vì (∆) song song với BD nên góc AME = góc ABD = 45 độ. Vì SA vuông góc với ABCD nên góc SAM = 90 độ. Vì SA = a√3 và góc SAM = 90 độ nên tam giác SAM là tam giác vuông cân tại A. Do đó, góc ASM = 45 độ. Vì góc ASM = góc AME = 45 độ nên tam giác ASM và tam giác AME đồng dạng. Vậy, ta có: AM/AS = AE/AM AM^2 = AS * AE AM^2 = (a√3) * (1/2 a) AM^2 = a^2 * √3 / 2 AM = a√3 / √2 AM = a√6 / 2 Ta có ME = 1/2 a Vậy, PM = AM - ME = (a√6 / 2) - (1/2 a) = (a√6 - a) / 2 Tương tự, ta có MQ = AM + ME = (a√6 / 2) + (1/2 a) = (a√6 + a) / 2 Vậy, thể tích SAPMQ = SABC * PM = a^2 * (a√6 - a) / 2 = a^3√6 / 2 - a^3 / 2

Hình bạn tự vẽ nha.
Xác định N: Qua M vẽ MN // BD (N thuộc SB)
Mà M là trung điểm SD → N là trung điểm SB
\(\frac{V_{S.CMN}}{V_{S.CDB}}=\frac{SM}{SD}\cdot\frac{SN}{SB}=\frac{1}{4}\) → VS.CMN = 1/4 * VS.CDB
Mà VS.CDB = 1/2 * VS.ABCD
→ VS.CDB = 1/8 * VS.ABCD
Gọi H là trung điểm AB → SH vg AB → SH vg (ABCD)\(V_{S.ABCD}=\frac{1}{3}\cdot SH\cdot S_{ABCD}=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2}\cdot a^2=\frac{a^3\sqrt{3}}{6}\)
\(\Rightarrow V_{S.CMN}=\frac{1}{8}\cdot\frac{a^3\sqrt{3}}{6}\)
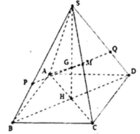
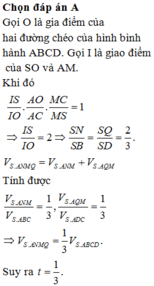
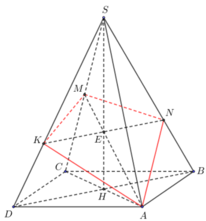
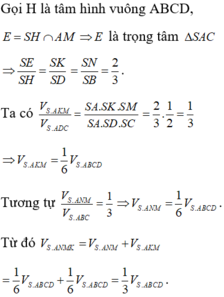

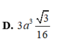

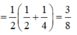

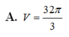
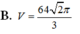
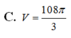


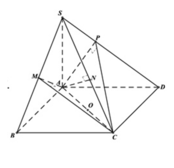
ình chóp S.ABCD là hình chóp đều nên chân H của đường cao SH chính là tâm của đáy. Mặt phẳng đi qua AM và song song với BD cắt mặt phẳng (SDB) theo một giao song song với BD, hay EF // BD.
Ta dựng giao tuyến EF như sau : Gọi I là giao điểm của AM và SH Qua I ta dựng một đường thẳng song song với BD, đường này cắt SB ở E và cắt SD ở F. Ta có góc SAH= 60°. Tam giác cân SAC có SA = SC và SAC = 60° nên nó là tam giác đều: I là giao điểm của các trung tuyến AM và SH nên:
