Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
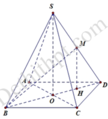
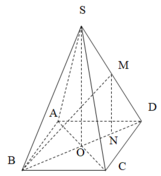
Gọi O là giao điểm của AC và B D ⇒ S O ⊥ A B C D Qua M kẻ đường thẳng song song với SO cắt BD tại H
⇒ M H ⊥ A B C D
Ta có M B ∩ A B C D = B và M H ⊥ A B C D
⇒ M B , A B C D ^ = M B , H B ^ = M B H ^
Ta có A C = A B 2 + B C 2 = a 2 ⇒ O A = A C 2 = a 2 2
Ta có S O = S A 2 − O A 2 = a 2 2 ⇒ M H = S O 2 = a 2 4
Ta có B H = 3 4 B D = 3 4 a 2 = 3 a 2 4
Ta có tan M B H ^ = M H B H = a 2 4 3 a 2 4 = 1 3 ⇒ tan M B , A B C D ^ = 1 3 .

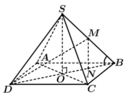
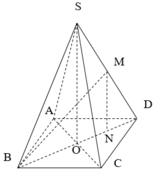
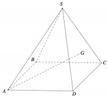
Gọi O là tâm hình vuông, suy ra ![]()
Trong tam giác vuông SOB tính được ![]()
Gọi N là trung điểm OD, suy ra MN//SO nên ![]() Khi đó
Khi đó
![]()
Xét tam giác vuông BNM ta có 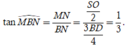
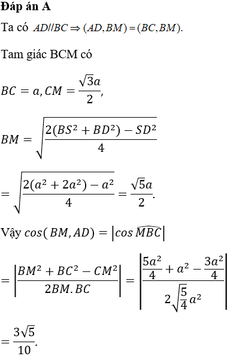
Chọn A.

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
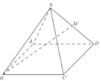

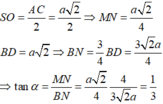
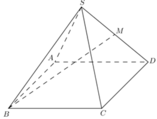


Do S.ABCD là hình chóp tứ giác đều ⇒ S O ⊥ A B C D . Gọi K là trung điểm OD, MK sẽ là đường trung bình trong tam giác ∆ S O D ⇒ M K ⊥ A B C D
⇒ B M ; A B C D = B M ; B K = M B K ⇒ tan M B K = M B M K M K = S O 2 = S A 2 - A O 2 2 = 2 a 4 B M = 3 4 B D A B 2 + A D 2 = 3 2 4 ⇒ tan M B K M K B K = 1 3
Đáp án cần chọn là D