Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là tâm hình vuông ABCD,M là trung điểm của SA
Mặt phẳng trung trực của đoạn thẳng SA cắt SO tại I
Điểm I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD bán kính R=IS
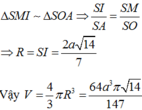
Đáp án C

Đáp án B.
Chiều cao khối chóp:
h = a 2 2 . tan 30 ° = a 6 6 .
Do đó
V = 1 3 a 2 . h = 1 3 a 2 . a 6 6 = 6 a 3 18 .

Chọn B.
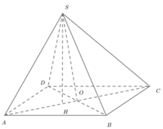
Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.




Do
![]()
và S A ' = 1 3 S A nên

Chọn: C
Chú ý: Công thức tỉ số thể tích trên chỉ áp dụng cho hình chóp tam giác.
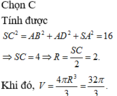

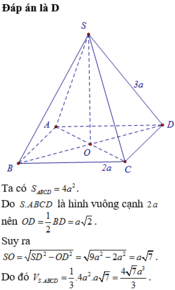
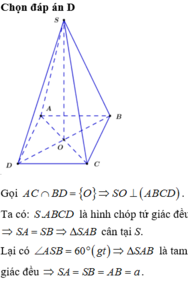
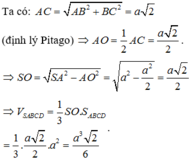
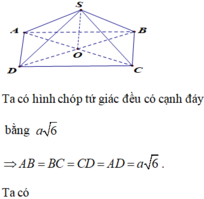
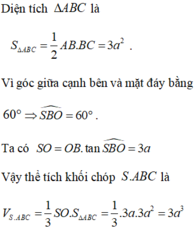
Đáp án D
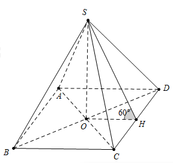
Gọi O là tâm của hình vuông ABCD.vì S.ABCD là hình chop đều nên S O ⊥ ( A B C D )
Từ giả thiết, ta có S O = S A 2 - O A 2 = a 10 2 .
Khối nón ngoại tiếp hình chóp S.ABCD có chiều cao h = S O = a 10 2 và bán kính đáy là r = O A = a 2 2 .
Suy ra V 2 = 1 3 πr 2 h = πa 3 10 12
Ta có SO là trục đường tròn ngoại tiếp hình vuông ABCD. Đường trung trực của SB nằm trong mặt phẳng (SBD) cắt SB, SO lần lượt tại M, I. Ta có IS = IB = IA = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có SI.IO = SM.SB ⇒ SI = S B 2 2 S O = 3 a 10 10
Suy ra V 1 = 4 3 π . ( SI ) 3 = 9 πa 3 10 25 . Do đó V 1 V 2 = 108 25