Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) `[S,BC,O]`:
Góc phẳng nhị diện `[S,BC,O`] là góc giữa mặt phẳng `(SBC)` và mặt phẳng `(SBO)`. Vì hình chóp tứ giác đều, nên mặt phẳng `(SBC)` và mặt phẳng `(SBO)` là hai mặt phẳng vuông góc với nhau. Do đó, góc phẳng nhị diện `[S,BC,O]` là góc vuông.
b) `[C,SO,B]`:
Góc phẳng nhị diện `[C,SO,B]` là góc giữa mặt phẳng `(CSO)` và mặt phẳng `(CSB)`. Vì hình chóp tứ giác đều, nên mặt phẳng `(CSO)` và mặt phẳng `(CSB)` là hai mặt phẳng vuông góc với nhau. Do đó, góc phẳng nhị diện` [C,SO,B]` là góc vuông.

a.
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(SA=SC=a\Rightarrow SA^2+SC^2=AC^2\)
\(\Rightarrow\Delta SAC\) vuông tại S (Pitago đảo)
\(\Rightarrow SA\perp SC\)
b.
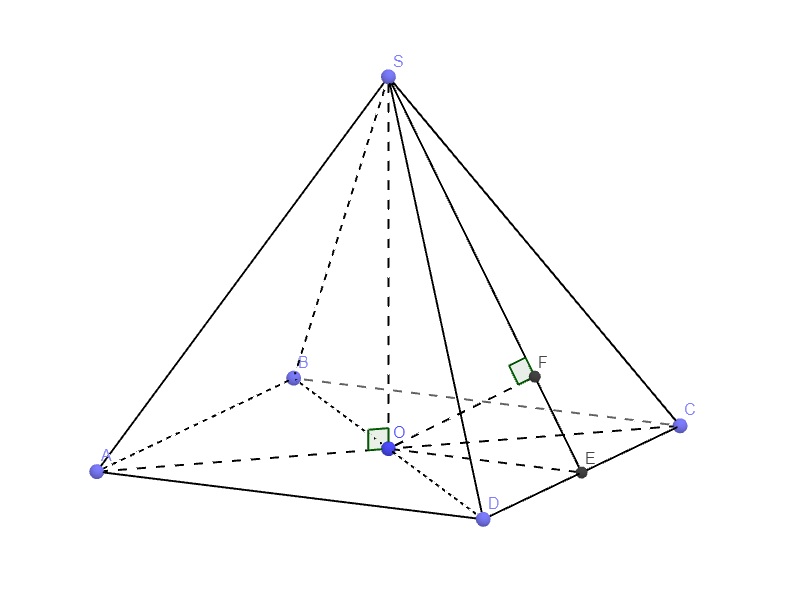
Gọi E là trung điểm CD \(\Rightarrow OE\perp CD\)
Chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\)
\(\Rightarrow CD\perp\left(SOE\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEO}\) là góc giữa mặt bên và đáy
\(OE=\dfrac{1}{2}BC=\dfrac{a}{2}\) (đường trung bình) ; \(SO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) (trung tuyến ứng với cạnh huyền)
\(\Rightarrow tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{2}\Rightarrow\widehat{SEO}=...\)
c.
Từ O kẻ \(OF\perp SE\Rightarrow OF\perp\left(SCD\right)\)
\(\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
Hệ thức lượng trong tam giác vuông SOE:
\(\dfrac{1}{OF^2}=\dfrac{1}{SO^2}+\dfrac{1}{OE^2}\Rightarrow OF=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{6}}{6}\)
\(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=2OF=\dfrac{a\sqrt{6}}{3}\)

1.
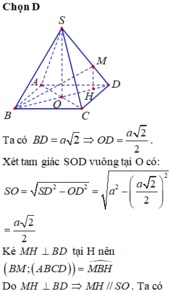
Đáp án C là đáp án đúng
Tất cả các cạnh bên của chóp đều bằng nhau, tất cả các cạnh đáy bằng nhau, nhưng tất cả các cạnh không chắc bằng nhau (cạnh bên có thể khác cạnh đáy)
2.
\(f'\left(x\right)=\dfrac{1}{2}cos^2x-\left(\dfrac{x-1}{2}\right)sin2x\)
\(f\left(x\right)-\left(x-1\right)f'\left(x\right)=0\Leftrightarrow\dfrac{x-1}{2}cos^2x-\dfrac{x-1}{2}cos^2x+\dfrac{\left(x-1\right)^2}{2}sin2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\sin2x=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\) đáp án D
3. \(y'=\sqrt{x}+\dfrac{x}{2\sqrt{x}}=\dfrac{3}{2}\sqrt{x}\)


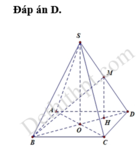

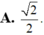

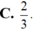
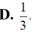
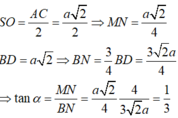



Đáp án A
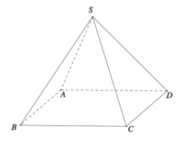
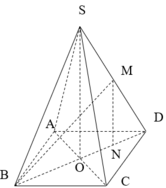
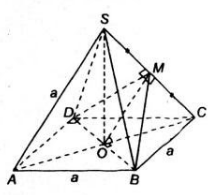
Gọi O là tâm mặt đáy có