Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình chóp tứ giác đều \(S.MNPQ\) có:
a) Mặt bên: \(SMN\); \(SNP\); \(SPQ\); \(SMQ\)
Mặt đáy: \(MNPQ\)
b) Các cạnh bên bằng nhau: \(SM = SN = SP = SQ = 15\)cm
Các cạnh đáy bằng nhau: \(MN = NP = PQ = MQ = 8\)cm

a: Mặt đáy: MNP
Mặt bên: SMP,SNP,SMN
Cạnh bên: SM,SN,SP
b: SN=SP=SM=4cm
NP=PQ=MN=3cm
c: 60 độ

a) Mặt đáy: \(ABCD\)
Các mặt bên: \(IAD\); \(IAB\); \(IBC\); \(ICD\)
b) Các cạnh bên bằng nhau: \(IB = IC = 18\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 14\)cm
c) Đoạn thẳng \(IH\) là đường cao của hình chóp

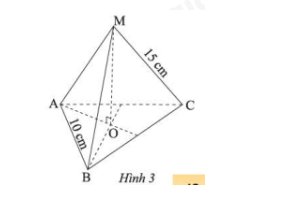
Các mặt bên là MAB, MAC, MBC
Các cạnh bên là MA = MB = MC = 15cm
Đường cao là MO
Các cạnh đáy là AB = AC = BC =10cm

Hình chóp tam giác đều \(S.DEF\) có:
a) Mặt bên: \(SDE\); \(SDF\); \(SEF\)
Mặt đáy: \(DEF\)
b) Các cạnh bên bằng nhau: \(SE = SF = SD = 5\)cm
Các cạnh đáy bằng nhau: \(ED = EF = DF = 3\)cm
c) Đáy \(DEF\) là tam giác đều nên ba góc ở đáy bằng nhau và bằng \(60^\circ \)

Kẻ A1H ⊥ AB, ta có:
A 1 I = 2,5cm; AJ = 5cm
Suy ra: AH = 2,5cm
Áp dụng định lí Pi-ta-go vào tam giác vuông A 1 H A , ta có:
A 1 A 2 = A 1 H 2 + A H 2 = 52 + 2,52 = 31,25
Suy ra: A 1 A = 31 , 25 ≈ 5,59 (cm)
Ta có: O 1 I = 2,5; OJ = 5cm.
Kẻ I I 1 ⊥ OJ, suy ra I 1 J = 2,5.
Áp dụng định kí Pi-ta-go vào tam giác vuông I I 1 J , ta có:
I J 2 = I I 1 2 + I 1 J 2
Suy ra: I I 1 2 = I J 2 + I 1 J 2 = 52 – 2,52 = 18,75
Suy ra: I I 1 = 18 , 75 ≈ 4,33 (cm)
Vậy O 1 O = I I 1 = 4,33 (cm)

a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))

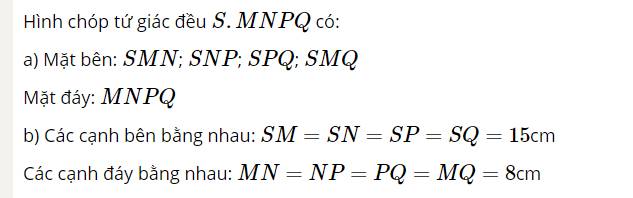



- Mặt bên: \(MAB\), \(MAC\), \(MBC\)
- Mặt đáy: \(ABC\)
- Đường cao: \(MO\)
- Độ dài cạnh bên: \(15\)cm
- Độ dài cạnh đáy: \(10\)cm