
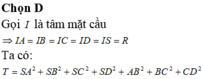
![]()

![]()

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

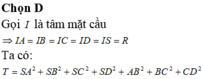
![]()

![]()


\(a=-1;b=0\)
\(c=0;d=-3\)
\(R=\sqrt{12+3^2}=2\)
\(\Rightarrow C\)
-Chúc bạn học tốt-

Lời giải:
Ta có:
\((S): x^2+y^2+z^2-2x-2y-2z=0\)
\(\Leftrightarrow (x-1)^2+(y-1)^2+(z-1)^2=3\)
Do đó mặt cầu \((S)\) có tâm \(O=(1,1,1)\) và \(R=\sqrt{3}\)
Khi đó, dễ dàng nhận thấy \(A\in (S)\)
Ta có \(S_{OAB}=\frac{OA.OB.\sin \angle AOB}{2}\leq \frac{OA.OB.1}{2}=\frac{3}{2}\) vì \(\sin AOB\leq 1\)
Dấu bằng xảy ra khi \(\angle AOB=90^0\)


Mặt cầu (S) có tâm I (1;0;-2) và bán kính R=2.
Đường thẳng d đi qua điểm N (2; 0; m-1) và có véc tơ chỉ phương ![]()
Điều kiện để d cắt (S) tại hai điểm phân biệt là d (I; (d))<R
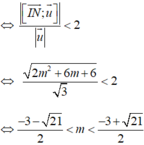
Khi đó, tiếp diện của (S) tại A và B vuông góc với IA và IB nên góc giữa chúng là góc (IA;IB).

Vậy T= {-3;0}. Tổng các phần tử của tập hợp T bằng -3.

4.
Gọi M là trung điểm CD, qua M kẻ đường thẳng song song AB
Gọi N là trung điểm AB, qua N kẻ đường thẳng song song AM
Gọi giao của 2 đường thẳng trên là O \(\Rightarrow\) O là tâm (S)
\(\Rightarrow AO=R=\sqrt{3}\)
Đặt \(AB=x;AC=y;AD=z\)
\(AN=\frac{AB}{2}=\frac{x}{2}\) ; \(AM=\frac{CD}{2}=\frac{1}{2}\sqrt{AC^2+AD^2}=\frac{1}{2}\sqrt{y^2+z^2}\)
Áp dụng Pitago: \(AO^2=AN^2+AM^2\)
\(\Rightarrow\frac{x^2}{4}+\frac{1}{4}\left(y^2+z^2\right)=3\Rightarrow x^2+y^2+z^2=12\)
\(V=\frac{1}{3}xyz\le\frac{1}{3}\left(\frac{x+y+z}{3}\right)^3\le\frac{1}{3}\left(\frac{\sqrt{3\left(x^2+y^2+z^2\right)}}{3}\right)^3=\frac{8}{3}\)
2.
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2-OA^2}=\frac{a}{2}\)
Áp dụng công thức từ câu 1:
\(R=\frac{SA^2}{2SO}=\frac{3a}{4}\)
3.
\(BC=AB\sqrt{2}=2a\)
Gọi H là hình chiếu của S lên (ABC) \(\Rightarrow\) H đồng thời là tâm đường tròn ngoại tiếp đáy
\(\Rightarrow\) H là trung điểm BC
\(\Rightarrow\widehat{SAH}=60^0\Rightarrow SH=AH.tan60^0=\frac{BC}{2}tan60^0=a\sqrt{3}\)
\(SA=\frac{AH}{cos60^0}=2a\)
\(\Rightarrow R=\frac{SA^2}{2SH}=\frac{2\sqrt{3}a}{3}\)
\(S=4\pi R^2=\frac{16\pi a^2}{3}\)