Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi E là giao điểm AB và CD
\(\Rightarrow E=\left(SAB\right)\cap\left(SCD\right)\)
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
b.
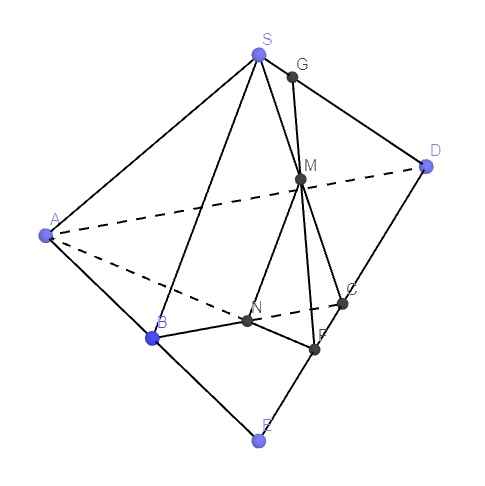
Do M là trung điểm SC, N là trung điểm BC
\(\Rightarrow MN\) là đường trung bình tam giác SBC
\(\Rightarrow MN||SB\)
Mà \(SB\in\left(SBD\right)\Rightarrow MN||\left(SBD\right)\)
c.
Trong mp (ABCD), nối AN cắt CD kéo dài tại F
Trong mp (SCD), nối FM kéo dài cắt SD tại G
\(\Rightarrow G=SD\cap\left(AMN\right)\)

a: Trong mp(ABCD), gọi N là giao điểm của AD và BC
\(N\in AD\subset\left(SAD\right);N\in BC\subset\left(SBC\right)\)
=>\(N\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SN\)
b: Gọi H là giao điểm của SG với CD
Xét ΔSCD có
G là trọng tâm
H là giao điểm của SG với DC
Do đó: H là trung điểm của DC
Chọn mp(SAH) có chứa MG
Trong mp(ABCD), gọi E là giao điểm của AH với BD
\(E\in AH\subset\left(SAH\right)\)
\(E\in BD\subset\left(SBD\right)\)
Do đó: \(E\in\left(SAH\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAH\right)\cap\left(SBD\right)\)
nên \(\left(SAH\right)\cap\left(SBD\right)=SE\)
Gọi K là giao điểm của MG với SE
=>K là giao điểm của MG với (SBD)

Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v



a, đề là gì vậy bạn
b, Xét (ABCD) kẻ AI giao CD tại I
Xét (SCD); (KAG) có
K là điểm chung t1 ; I là điểm chung t2
=> KI là giao tuyến 2 mp
=> Nối IK cắt SD tại M
c, Ta có M = (SAIM) giao (GHK)
E = (HKAI) giao (GHK)
G = (HKAI) giao (SAIM)
mà ME ko song song vs MG
=> M;E;G thẳng hàng

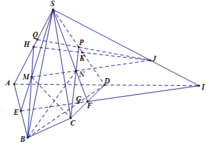
Qua G kẻ đường thẳng song song AC lần lượt cắt AD, AB, BC tại E, F, N.
là giao tuyến của (GHK) và (ABCD)
Nối EH kéo dài cắt SD tại M là giao điểm SD và (NHK)
c/ Gọi P là giao điểm của FN kéo dài và CD
Ta có , mà BD qua trung điểm của AC qua trung điểm của EP là trung điểm EP
Mà MG qua trung điểm của EP MG qua trung điểm của HK hay G,M,E thẳng hàng

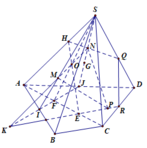

a/ Một kinh nghiệm khi đề bài cho dữ kiện về trọng tâm thì vẽ hết 3 đường trung tuyến ra, sẽ rất dễ nhìn
Ta có SG là đường trung tuyến của tam giác SCD, kéo dài SG cắt CD ở K=> \(MG\subset\left(SAK\right)\)
\(\left\{{}\begin{matrix}A\in SA\subset\left(SAK\right)\\A\in AB\subset\left(ABCD\right)\end{matrix}\right.\Rightarrow A=\left(SAK\right)\cap\left(ABCD\right)\)
\(\left\{{}\begin{matrix}K\in SK\subset\left(SAK\right)\\K\in CD\subset\left(ABCD\right)\end{matrix}\right.\Rightarrow K=\left(SAK\right)\cap\left(ABCD\right)\)
\(\Rightarrow\left(SAK\right)\cap\left(ABCD\right)=AK\)
\(AK\cap MG=\left\{I\right\}\Rightarrow MG\cap\left(ABCD\right)=\left\{I\right\}\)
b/ \(BN\subset\left(SBD\right)\)
\(\left(SAG\right)\equiv\left(SAK\right)\)
\(AK\cap BD=\left\{H\right\}\Rightarrow H=\left(SBD\right)\cap\left(SAK\right)\)
\(\Rightarrow\left(SAG\right)\cap\left(SAK\right)=SH\)
\(SH\cap BN=\left\{O\right\}\Rightarrow BN\cap\left(SAG\right)=\left\{O\right\}\)
a/ Một kinh nghiệm khi đề bài cho dữ kiện về trọng tâm thì vẽ hết 3 đường trung tuyến ra, sẽ rất dễ nhìn
Ta có SG là đường trung tuyến của tam giác SCD, kéo dài SG cắt CD ở K=> \(MG\subset\left(SAK\right)\)
\(\left\{{}\begin{matrix}A\in SA\subset\left(SAK\right)\\A\in AB\subset\left(ABCD\right)\end{matrix}\right.\Rightarrow A=\left(SAK\right)\cap\left(ABCD\right)\)
\(\left\{{}\begin{matrix}K\in SK\subset\left(SAK\right)\\K\in CD\subset\left(ABCD\right)\end{matrix}\right.\Rightarrow K=\left(SAK\right)\cap\left(ABCD\right)\)
\(\Rightarrow\left(SAK\right)\cap\left(ABCD\right)=AK\)
\(AK\cap MG=\left\{I\right\}\Rightarrow MG\cap\left(ABCD\right)=\left\{I\right\}\)
b/ \(BN\subset\left(SBD\right)\)
\(\left(SAG\right)\equiv\left(SAK\right)\)
\(AK\cap BD=\left\{H\right\}\Rightarrow H=\left(SBD\right)\cap\left(SAK\right)\)
\(\Rightarrow\left(SAG\right)\cap\left(SAK\right)=SH\)
\(SH\cap BN=\left\{O\right\}\Rightarrow BN\cap\left(SAG\right)=\left\{O\right\}\)