Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
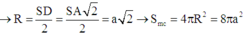

Hướng dẫn: D
+ Gọi x > 0 là cạnh của hình vuông ABCD và H là trung điểm cạnh AD
+ Dễ dàng chứng minh
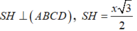
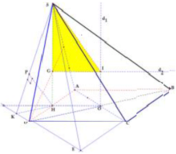
+ Gọi O = AC ∩ BD và G là trọng tâm ∆ A S D , đồng thời d 1 , d 2 lần lượt là 2 trục đường tròn ngoại tiếp ABCD, ∆ S A D ( d 1 qua O và // SH, d 2 qua G và //AB)
⇒ I = d 1 ∩ d 2 là tâm mặt cầu ngoại tiếp khối chóp S. ABCD ⇒ R = SI
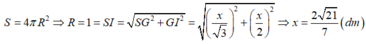
(trong video bài giảng chữa đề, phần này Thầy dùng công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp trong trường hợp chóp có mặt bên vuông góc với mặt đáy).
+ Gọi E là điểm thỏa ADEC là hình bình thành
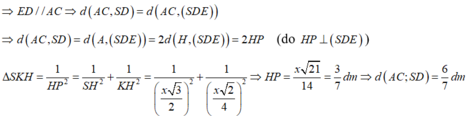

Đáp án A
Gọi H là trung điểm của AB, tam giác SAB cân tại S do đó SH⊥AB mà (SAB)⊥ (ABCD) nên SH⊥ (ABCD). Góc giữa SC và đáy là SCH =600.
Tam giác BHC vuông tại B nên
![]()
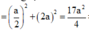
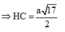
Tam giác SHC vuông tại H nên SH = SC.tanSCH ![]()
Do vậy 

Chọn đáp án D
Gọi O là tâm của hình chữ nhật ABCD và I là trung điểm của SC. Khi đó OI ⊥ (ABCD)
⇒ IA = IB = IC = ID với ∆ S A C vuông tại A, IA = IS = IC. Do đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD suy ra IA = a 2 ⇒ SC = 2a 2 . Mặt khác AC là hình chiếu của SC trên mặt phẳng (ABCD).
![]()
Suy ra ∆ S A C vuông cân
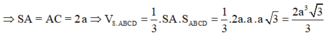
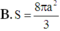
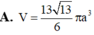
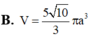
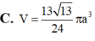
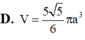

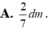
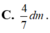
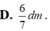


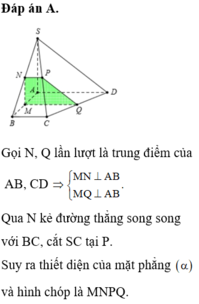


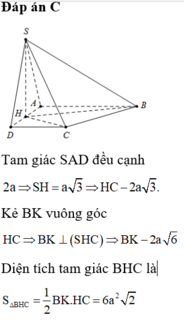
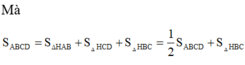
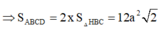
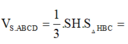
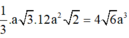

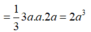
Đáp án A.
Trong mặt phẳng (ABCD) gọi: H là trung điểm AD.
H là trung điểm AD.
Gọi I,J lần lượt là trung điểm của BC và G là trọng tâm ∆ SAD
Đường thẳng d qua O và vuông góc với (ABCD) gọi là trục của đường tròn ngoại tiếp đáy (ABCd).
∆ qua G và vuông góc với (SAD) là trục của đường tròn ngoại tiếp (SAD).
Trong mặt phẳng (SHI), gọi I = ∆ ∩ d
=> J cách đều các đỉnh của hình chóp
=> J là tâm mặt cầu ngoại tiếp S.ABCD có bán kính
R = JD =
Có