K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
Đề bài thiếu 1 dữ liệu nữa (ví dụ SA vuông góc mặt đáy)

AH
Akai Haruma
Giáo viên
8 tháng 12 2021
Lời giải:
$SA\perp (ABCD)$ nên $45^0=\angle (SB, (ABCD))=\angle (SB, AB)=\widehat{SBA}$
$\Rightarrow SA=AB=5$ (cm)
Thể tích khối chóp $S.ABCD$:
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.5.5^2=\frac{125}{3}$ (cm3)

CM
3 tháng 3 2019
Đáp án A
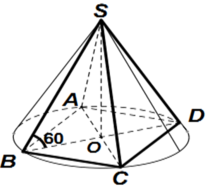
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)


CM
10 tháng 5 2019
Chọn A.
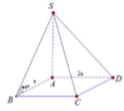
Ta có: ![]()
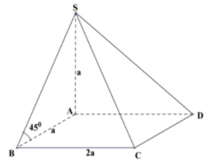
![]() Do tam giác SAB vuông cân tại A nên SA = AB = a.
Do tam giác SAB vuông cân tại A nên SA = AB = a.
Vậy ![]()

CM
9 tháng 9 2017
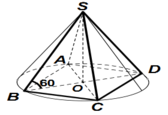
Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
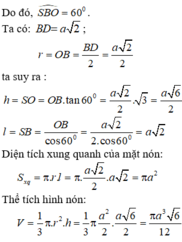
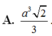
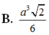
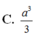

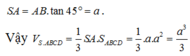
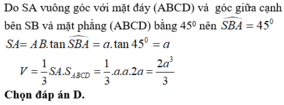
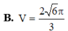

a.
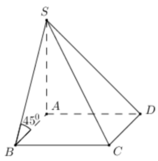
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và đáy
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3}{3}\)
\(SB=SD=\sqrt{SA^2+AB^2}=a\sqrt{2}\)
\(S_{xq}=\dfrac{1}{2}SA.AD+\dfrac{1}{2}SA.AB+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=a^2\left(\sqrt{2}+1\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và đáy
\(\Rightarrow\widehat{SDA}=60^0\)
\(\Rightarrow SA=AD.tan60^0=a\sqrt{3}\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3\sqrt{3}}{3}\)
\(SB=SD=\sqrt{SA^2+AD^2}=2a\)
\(S_{xq}=\dfrac{1}{2}SA.AB+\dfrac{1}{2}SA.AD+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=3a^2\)