Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Hướng dẫn giải:
Ta có
![]()
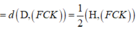
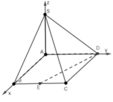
Kẻ H I ⊥ C K , H J ⊥ F I
![]()
Ta có H I = 2 a 5 5
![]()
⇒ S B = a 3
![]()
⇒ H F = a 2 2
Ta có 1 H J 2 = 1 H I 2 + 1 H F 2 = 13 4 a 2
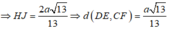

Đáp án A
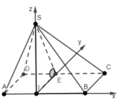
Gắn trục tọa độ Axyz với A là gốc tọa độ sao cho:
Tia Ax trùng tia AB; tia Ay trùng tia AD; tia Az trùng tia AS.
Khi đó:
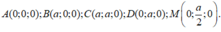
Gọi O là tâm hình vuông ABCD.
Do góc giữa mặt phẳng(SBD)và (ABCD) bằng 60 o nên S O A ⏞ = 60 o
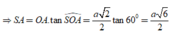
⇒ S 0 ; 0 ; a 6 2
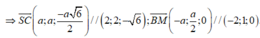
Mặt phẳng (P) chứa SC và song song với BM có vecto pháp tuyến là ( 6 ; 2 6 ; 6 ) / / 1 ; 2 ; 6 nên có phương trình:
x + 2 y + 6 z - 3 a = 0
Do đó: d ( S C , B M ) = d ( B ; ( P ) ) = 2 a 11 (đvđd).

Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

Đáp án A
Hướng dẫn giải: Ta có:
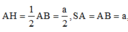
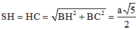
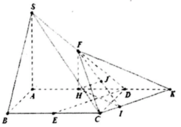
Có A H 2 + S A 2 = 5 a 2 4 = S H 2 ⇒ ∆ S A H vuông tại A
Do đó mà S A ⊥ ( A B C D ) nên
![]()
(Mặt phẳng (SAB) vuông góc với đáy (ABCD))
Trong tam giác vuông SAC, có
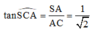

Lớp 12 thì chúng ta tọa độ hóa cho đơn giản
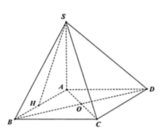
Gọi O là trung điểm AB \(\Rightarrow SO\perp\left(ABCD\right)\)
\(SO=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(AO=BO=\dfrac{a}{2}\)
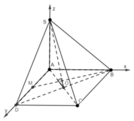
Đặt hệ trục Oxyz vào chóp, với gốc O trùng O, tia Oz trùng tia OS, tia Ox trùng tia OB, tia Oy trùng tia ON (với N là trung điểm CD). Quy ước \(\dfrac{a}{2}\) là 1 đơn vị độ dài
Ta được tọa độ các điểm: \(S\left(0;0;\sqrt{3}\right)\) ; \(C\left(1;2;0\right)\) ; \(A\left(-1;0;0\right)\) ; \(D\left(-1;2;0\right)\)
Do M là trung điểm SD \(\Rightarrow M\left(-\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\)
\(\overrightarrow{AM}=\left(\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\) ; \(\overrightarrow{SC}=\left(1;2;-\sqrt{3}\right)\) ; \(\overrightarrow{AC}=\left(2;2;0\right)\)
\(d\left(AM;SC\right)=\dfrac{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right].\overrightarrow{AC}\right|}{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right]\right|}=\dfrac{2\sqrt{5}}{5}=\dfrac{a\sqrt{5}}{5}\)
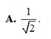
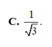

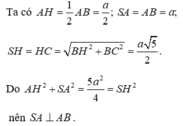

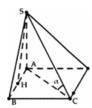
Đáp án A
Xét ∆ S B C vuông tại B,nên dễ tính được S B = a 3
Từ đó suy ra S A = a 2
Gắn trục tọa độ Axyz với A là gốc tọa độ sao cho:
Tia Ax trùng tia AB; tia Ay trùng tia AD; tia Az trùng tia AS.
Khi đó:
Phương trình mặt phẳng qua DE và song song với SC là:
Do đó, khoảng cách giữa hai đường thẳng ED và SC là:
d ( E D ; S C ) = d ( S ; ( P ) ) = a 38 19