

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
Gọi H là chân đường vuông góc hạ từ đỉnh S lên mặt phẳng (ABC), khi đó ta chứng minh được H là trung điểm của BC. Gọi M là trung điểm của AB khi đó từ giả thiết ta có: ![]()
Đặt AB = x ta tính được: 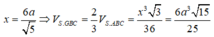

Lời giải:
Lấy $H$ là trung điểm $AB$ thì do $SAB$ cân tại $S$ nên $SH\perp BH$
$BH$ là giao tuyến của $(SAB), (ABCD)$; (SAB)\perp (ABCD)$ nên $SH\perp (ABCD)$
$\Rightarrow (SC, (ABCD))=(SC, CH)=\widehat{SCH}=45^0$
$\Rightarrow SH=CH=\sqrt{BC^2+BH^2}=\sqrt{(2a)^2+(\frac{a}{2})^2}=\frac{\sqrt{17}}{2}a$
\(V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{17}}{2}a.a.2a=\frac{\sqrt{17}}{3}a^3\)

G�c ?: G�c gi?a E, C, H G�c ?: G�c gi?a E, C, H ?o?n th?ng a: ?o?n th?ng [A, D] ?o?n th?ng b: ?o?n th?ng [A, B] ?o?n th?ng e: ?o?n th?ng [B, C] ?o?n th?ng f: ?o?n th?ng [C, D] ?o?n th?ng h: ?o?n th?ng [E, H] ?o?n th?ng i: ?o?n th?ng [E, A] ?o?n th?ng j: ?o?n th?ng [E, B] ?o?n th?ng k: ?o?n th?ng [E, D] ?o?n th?ng l: ?o?n th?ng [E, C] ?o?n th?ng m: ?o?n th?ng [H, C] A = (-1.48, 1.8) A = (-1.48, 1.8) A = (-1.48, 1.8) D = (2.3, 1.8) D = (2.3, 1.8) D = (2.3, 1.8) B = (-3.12, -0.08) B = (-3.12, -0.08) B = (-3.12, -0.08) ?i?m C: Giao ?i?m c?a c, d ?i?m C: Giao ?i?m c?a c, d ?i?m C: Giao ?i?m c?a c, d ?i?m H: (A + B) / 2 ?i?m H: (A + B) / 2 ?i?m H: (A + B) / 2 ?i?m E: ?i?m tr�n g ?i?m E: ?i?m tr�n g ?i?m E: ?i?m tr�n g
Kẻ SH vuông góc với AB. Do (SAB) vuông góc với đáy nên hình chiều của S trên (ABCD) chính là H.
Mặt khác tam giác SAB cân tại S nên H là trung điểm của AB.
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\dfrac{a^2}{4}+a^2}=\dfrac{a\sqrt{5}}{2}\)
Góc giữa SC và đáy là góc SCH nên \(\widehat{SCH}=45^0\)
\(SH=CH.\tan 45^0=\dfrac{a\sqrt{5}}{2}\)
\(S_{ABCD}=a^2\)
Vậy \(V_{SABCD}=\dfrac{1}{3}.SH.S_{ABCD}=\dfrac{a^3\sqrt{5}}{6}\)
bh tính kiểu gì vậy bạn
mà bạn xác định góc giữa sc và mặt đáy phải là góc SCA chứ
giải thích hộ mình với

Lời giải:
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp (ABCD)$
Vì $SA\perp (ABCD)$ nên $SA\perp CB$
Mà: $AB\perp CB$
$\Rightarrow CB\perp (SAB)$
$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$
$\Rightarrow SB=CB=a$
$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)