Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
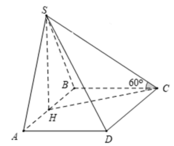
Ta có: H C = B H 2 + B C 2 = a 2
S H = H C . tan S C H = a 2 . tan 60 ∘ = a 6 A C = B A 2 + B C 2 = a 5 , S B = S H 2 + H B 2 = a 7
Ta có: S B → . A C → = S H → + H B → . A C → = H B . A C . cos B A C
⇔ S B → . A C → = H B . A C . A B A C = 2 a 2 S B . A C = a 7 . a 5 = a 2 35 ⇒ c os S B , A C = S B → . A C → S B . A C = 2 a 2 a 2 35 ⇒ S B , A C = 70 o 14 ' 28 , 22 ' '

Đáp án B.
Ta có A D / / B C , A D ∉ ( S B C ) , B C ⊂ ( S B C ) ⇒ A D / / ( S B C )
⇒ d ( A D ; S C ) = d ( A D ; ( S B C ) ) = d ( D ; ( S B C ) ) .
Qua I kẻ đường thẳng song song với AD, cắt CD tại H.
Suy ra I H ⊥ C D
Từ C D ⊥ I H , C D ⊥ S I ⇒ C D ⊥ ( S I H ) ⇒ C D ⊥ S H .
Suy ra ( S C D ) , ( A B C D ) ⏜ = S H , I H ⏜ = S H I ⏜ ⇒ C D ⊥ S H
S I = H I . tan S H I ⏜ = a . tan 60 ° = a 3 ⇒ V S . B C D = 1 2 S A B C D = a 3 3 6 .
Lại có V S . B C D = 1 3 . S ∆ S B C . d ( D ; ( S B C ) ) ⇒ d ( D ; ( S B C ) = 3 V S . B C D S ∆ S B C (1)
Từ I B = 2 3 A B = 2 3 a ⇒ S B = S I 2 + I B 2 = a 3 2 + 2 a 3 2 = a 31 3 .
Từ B C ⊥ A B , B C ⊥ S I ⇒ B C ⊥ ( S A B ) ⇒ B C ⊥ ( S A B ) ⇒ B C ⊥ S B ⇒ ∆ S B C vuông tại B.
Suy ra S ∆ S B C = 1 2 S B . S C = 1 2 . a 31 3 . a = a 2 31 6 (2)
Từ (1) và (2), suy ra d ( D ; ( S B C ) ) = 3 a 3 3 6 a 2 31 6 = 3 a 3 31 = 3 39 31 a
Vậy d ( A D ; S C ) = d ( D ; ( S B C ) ) = 3 93 31 a

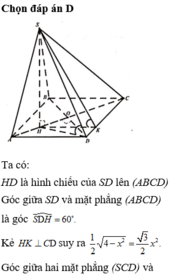
Đáp án D
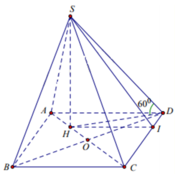
Gọi I ∈ C D sao cho H I / / A D .
Ta có H I A D = C H C A ⇔ H I = A D . C H C A = 2 a . 3 4 = 3 a 2 .
Và H D = D O 2 + H O 2 = D O 2 + D O 2 4 = D O 5 2 .
Mà 2 D O 2 = 4 a 2 ⇒ D O = a 2
⇒ H D = a 2 . 5 2 = a 10 2 ⇒ S H = H D . tan 60 ∘ = a 30 2 .
Vậy α = S I H ^ ⇒ tan α = S H H I = a 30 2 3 a 2 = 30 2 .

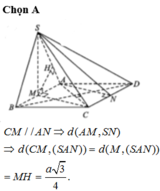
Chọn A
Chọn hệ trục tọa độ như hình vẽ, ta có H(0;0;0) , B(-a; 0; 0) và C(-a; a; 0), E(0; a; 0), S(0; 0; a 3 )

Ta có B E → = ( a ; a ; 0 ) , S C → = - a ; a ; - a 3 , E C → = ( - a ; 0 ; 0 )
Khi đó , B E → , S C → = ( - a 2 3 ; a 2 3 ; 2 a 2 )
Khoảng cách giữa BE và SC là





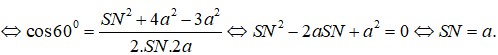

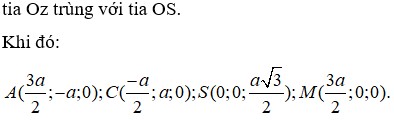
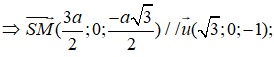
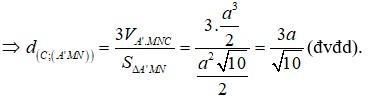



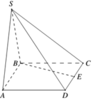
Đáp án là A