Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
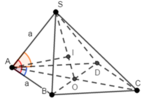
Ta có: SA = SB = SC =a
![]()
![]()
![]()
⇒ ∆ S B D đ ề u
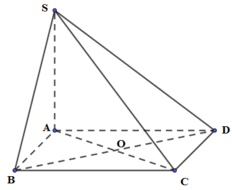
Gọi O là tâm hình thoi ABCD, I là tâm tam giác đều SBD cạnh a.
Vì AS = AB = AD
![]()
Dễ dàng tính được
![]()
Xét ∆ A I O vuông tại I có:
![]()
⇒ V A . S B D = 1 3 . A I . S S B D = a 2 3 12 (đvtt)

Lời giải:
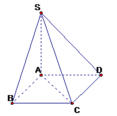
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp (ABCD)$
Vì $SA\perp (ABCD)$ nên $SA\perp CB$
Mà: $AB\perp CB$
$\Rightarrow CB\perp (SAB)$
$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$
$\Rightarrow SB=CB=a$
$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)

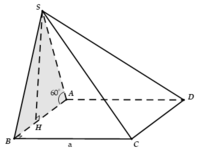
a) Dễ dàng chứng minh tam giác ABC và ACD đều
Suy ra AC=a, SA= AC.tan(gócSCA)=a.tan(600)
\(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.a\sqrt{3}.a^2.\frac{\sqrt{3}}{2}=\frac{a^3}{2}\)
b) Có 2 cách làm để tìm khoảng cách từ H đến mp(SCD), nhưng bạn nên chọn phương pháp tọa độ hóa cho dễ
Chọn A làm gốc tọa độ , các tia AD, AI, AS lần lượt trùng tia Ax, Ay, Az
Có ngay tọa độ các điểm \(S\left(0;0;a\sqrt{3}\right)\) , \(D\left(a;0;0\right)\) , \(I\left(0;\frac{a\sqrt{3}}{2};0\right)\)
\(\Rightarrow C\left(\frac{a}{2};\frac{a\sqrt{3}}{2};0\right)\)
theo số liệu đã cho, dễ xác định được điểm H chia đoạn SI với tỷ lệ 2:1
\(\Rightarrow H\left(0;\frac{a}{\sqrt{3}};\frac{a}{\sqrt{3}}\right)\)
Bây giờ chỉ cần viết pt (SCD) là tính được ngay khoảng cách từ H đến SCD
\(\left(SCD\right):\sqrt{3}x+y+z-\sqrt{3}=0\)
\(d\left(H\text{/}\left(SCD\right)\right)=\frac{a\sqrt{3}}{\sqrt{5}}\)
Bạn ơi bạn chỉ mình cách bình thường được ko? Vì mình chưa học tọa độ hóa.
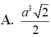
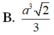
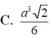
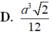
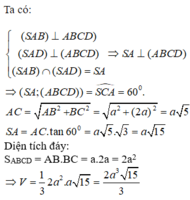


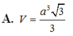
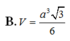
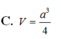
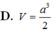
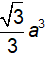
Đáp án C